You Cannot Feed Two Birds with One Score: the Accuracy-Naturalness Tradeoff in Translation


Gergely Flamich

07/08/2025

gergely-flamich.github.io

In Collaboration With

the goals of translation

Accuracy

Translation carries the meaning of the source text

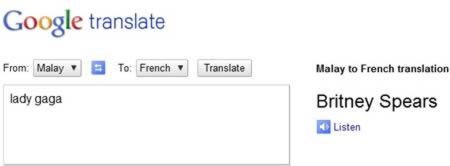
Naturalness

Translation sounds good in target language

measuring translation quality

Ingredients

  • Have dataset of source text
  • Have dataset of human reference translations
  • Translation system \(Q_{y \mid x}\) to translate source text

Human Evaluations

Multidimensional Quality Metrics (MQM) [2]

Classic Automated Metrics

Examples: BLEU, chrF

Purely symbolic: compare to human reference translation

✅ simple

❌ limited by the human reference

Neural Metrics

Examples: MetricX, Comet

Large language model-based: predict MQM scores

✅ Jointly assess accuracy and naturalness

Feeding Two birds with one score

Feeding Two birds with one score

Should we assess accuracy and naturalness jointly?

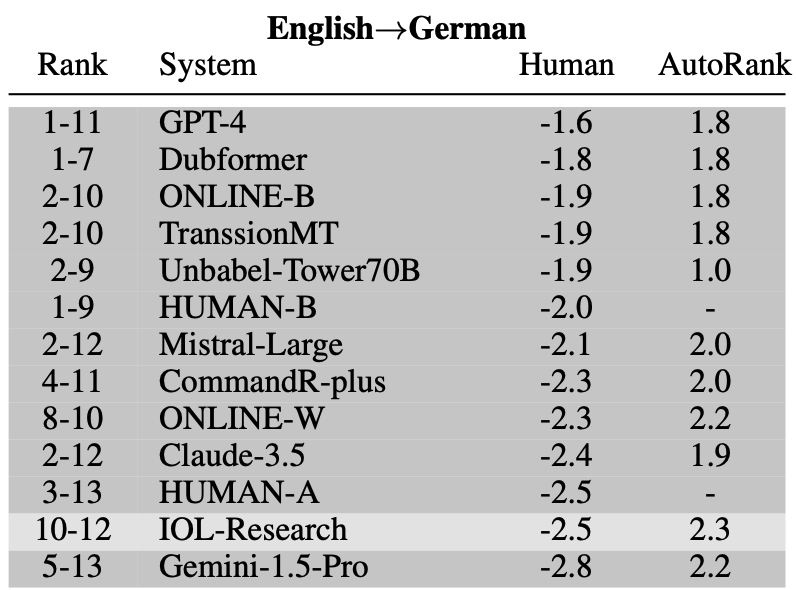
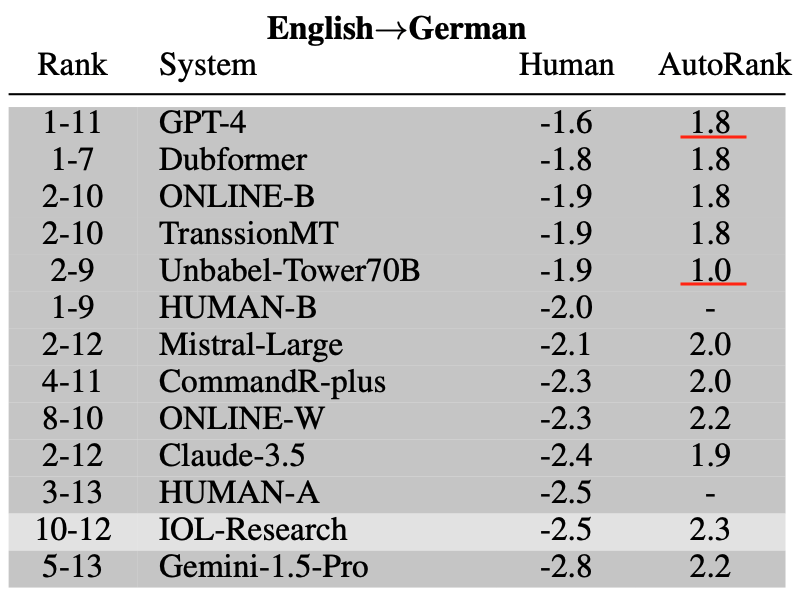
Table from WMT24 findings paper [1].

where we are

  • No formal notion of accuracy or naturalness
  • Their interaction not well understood
  • Community uses single-score assessments
  • Results don't seem to align with human evals

Information theory to the rescue

💡 Blau and Michaeli [3] already solved a similar issue!

Accuracy \(\leftrightarrow\) Distortion

Naturalness \(\leftrightarrow\) Realism/Distinguishability

Ingredients

  • Source sentence \(x\)
  • Translation system \(Q_{y \mid x}\)
  • Reference translation \(y^r \sim Q_{y \mid x}^{\mathrm{human}}\)
  • Hypothesis/candidate \(y^c \sim Q_{y \mid x}\)

Accuracy

  • Distortion metric: \(\Delta(x, y^r, y^c) \geq 0\)
  • Accuracy: average negative distortion

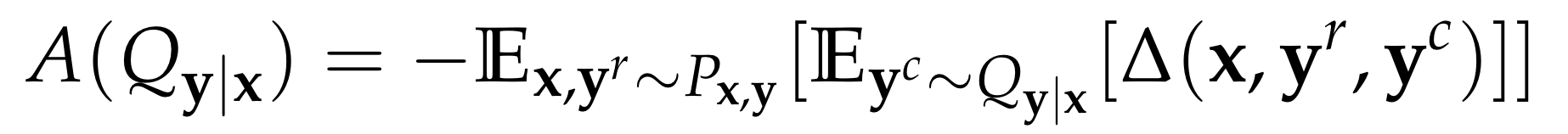
Naturalness: Intuition

Naturalness: Definition I

  • Identify naturalness with distinguishability
  • We pick a reference distribution \(R_y\)

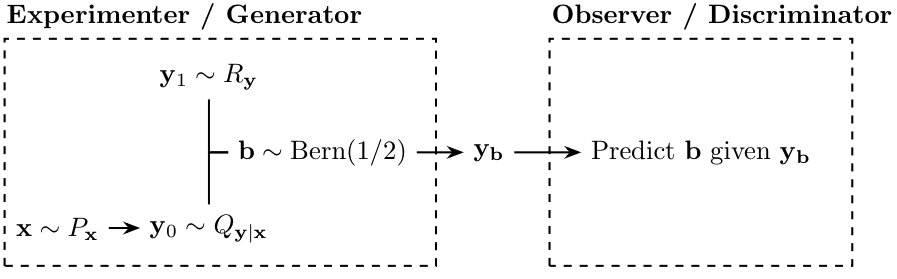
Naturalness: Definition II

  • Translation marginal \(Q_y\)
  • Distinguishability is equivalent to statistical distance \(D(Q_y, R_y)\)

\[ N(Q_{y \mid x}) = -D(Q_y, R_y) \]

the divergence

Let \(P(f) = \mathbb{E}_{X \sim P}[f(X)]\)

Integral probability metric (IPM):

\[ \mathrm{IPM}_{\mathcal{F}}[Q \Vert P] = \sup_{f \in \mathcal{F}}\lvert Q(f) - P(f) \rvert \]

Optimal critic \(f^\star\)

\[ f^\star = \mathrm{argmax}_{f \in \mathcal{F}}\lvert Q(f) - P(f) \rvert \]

The Equivalence

Set \(\epsilon = \mathbb{P}[b = 1]\). Then:

\begin{gather*} L(b, \alpha) = \begin{cases} -\alpha / \epsilon & \text{if } b = 1 \\ \alpha / (1 - \epsilon) & \text{if } b = -1 \end{cases} \end{gather*}

Then:

\begin{gather*} R_{\mathcal{F}}^L = \inf_{f \in \mathcal{F}}\mathbb{E}[L(\mathbf{b}, f(\mathbf{y}_{\mathbf{b}}))] = -\mathrm{IPM}_{\mathcal{F}}[Q \Vert P] \end{gather*}

Are perfect accuracy and naturalness the same?

Perfect naturalness \(\Rightarrow\) perfect accuracy?

Perfect accuracy \(\Rightarrow\) perfect naturalness?

  • No, according to Blau and Michaeli's setup [3]
  • No, according to our setup [4]

what is the tradeoff like?

Accuracy-naturalness function:

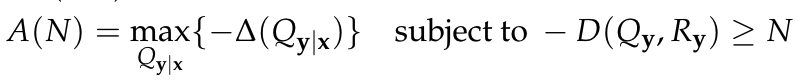
  • \(A(N)\) is non-increasing
  • If \(D\) convex in first slot, then \(A(N)\) concave

Approximating the curve

💡 Use LLM scores to judge the translations!

🤔 Does this correspond to some \(D(Q, P)\)?

EN \(\to\) DE: I’ve wanted to fly since I was a child.

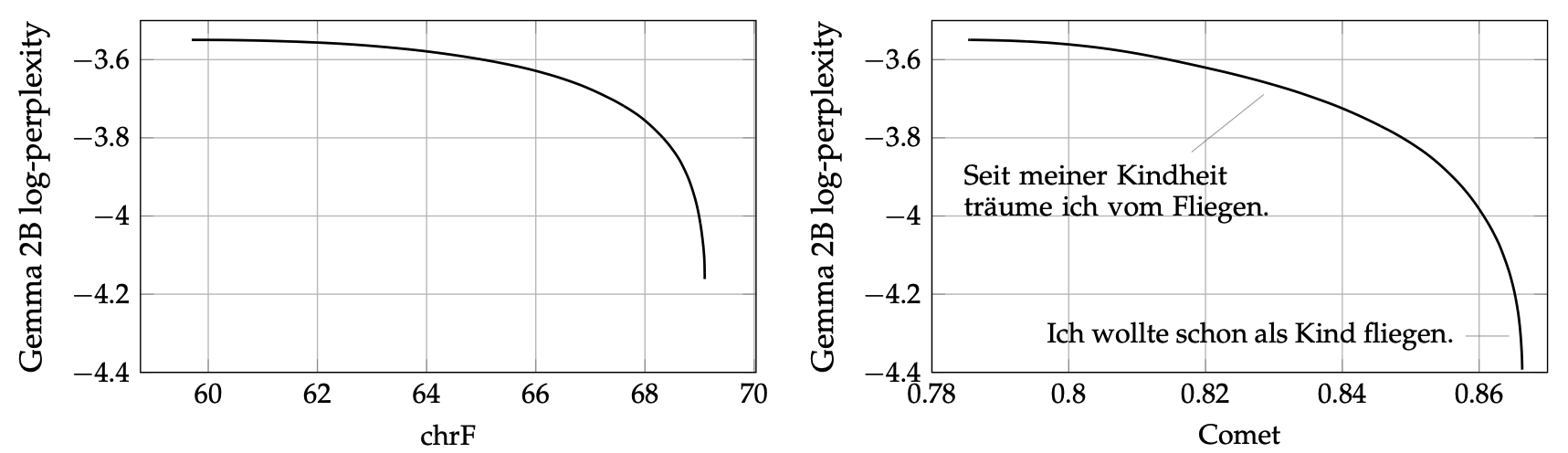
where is the SOTA?

Close to the curve, accuracy and naturalness anti-correlate

where is the SOTA?

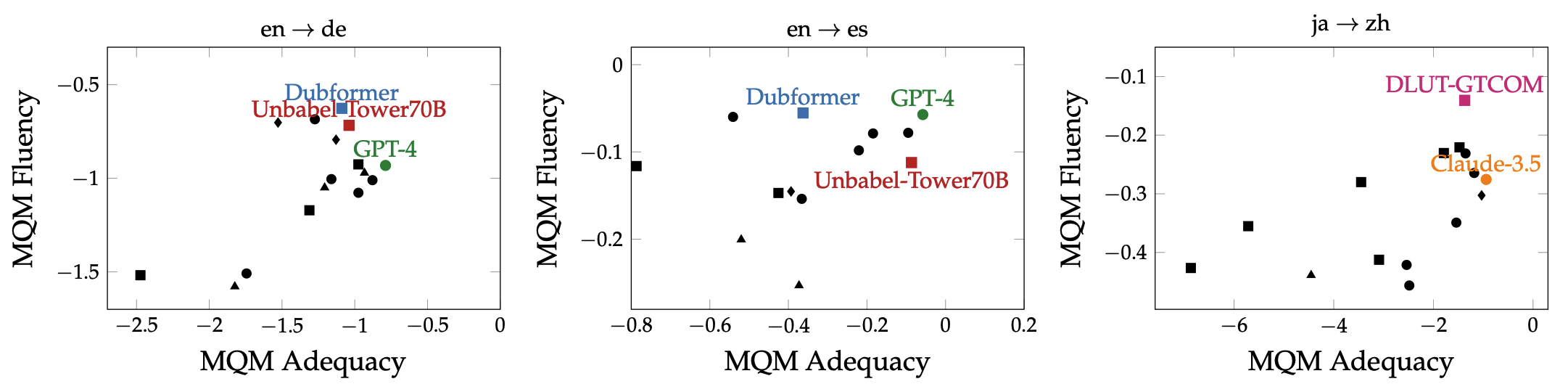
the issue and the fix

\(\mathrm{IPM}_{\mathcal{F}}[Q \Vert P] = \sup_{f \in \mathcal{F}}\lvert Q(f) - P(f) \rvert\)

❌ \(f^\star\) depends on \(Q\)!

✅ Fix: average instead of maximising

Let \(f \sim \mathcal{P}\)

\begin{align*} D_p(Q, P \mid \mathcal{P}) &= \mathcal{P}(\vert Q - P \vert^p)^{1/p} \\ &= \mathbb{E}_{f \sim \mathcal{P}}[\vert Q(f) - P(f) \vert^p]^{1/p} \end{align*}

Some interesting properties

✅ \(D_p\) a metric under some sensible conditions

✅ Can estimate without knowing \(Q\): \[ D_1(Q, P \mid \mathcal{P}) \approx \frac{1}{N} \sum_{n = 1}^N \left(\sum_{m = 1}^{M_Q}\frac{f_n(X_m)}{M_Q} - \sum_{m = 1}^{M_P}\frac{f_n(Y_m)}{M_P}\right) \]

✅ When \(\mathcal{P}\) is a GP, \(D_2\) corresponds to MMD

contributions

  • Proposed a formal definition of accuracy and naturalness
  • Extended the theory of Blau and Michaeli
  • Showed that tradeoff must exist in practice
  • Assessed the performance of the current state-of-the-art
  • Showed connection between no-reference metrics and statistical distances

References I

  • [1] Kocmi et al. (2024). Findings of the WMT24 general machine translation shared task: the LLM era is here but mt is not solved yet. In Proceedings of the Ninth Conference on Machine Translation (pp. 1-46).
  • [2] Freitag et al. (2021). Experts, errors, and context: A large-scale study of human evaluation for machine translation. Transactions of the Association for Computational Linguistics, 9, 1460-1474.

References II

  • [3] Yochai Blau and Tomer Michaeli. The perception-distortion tradeoff. In Proceedings of the IEEE conference on computer vision and pattern recognition, pp. 6228–6237, 2018.
  • [4] F et al. (2025). You Cannot Feed Two Birds with One Score: the Accuracy-Naturalness Tradeoff in Translation. arXiv preprint arXiv:2503.24013.

References III

  • [5] Sriperumbudur et al. (2009). On integral probability metrics,φ-divergences and binary classification. arXiv preprint arXiv:0901.2698.