Relative Entropy Coding with Greedy Poisson Rejection Sampling


Gergely Flamich

29/09/2023

1. In Collaboration With

2. What is Relative Entropy Coding?

2.1. Lossy compression

transform_encoding.png

transform_decoding.png

2.2. Transform Coding as a Channel

Get an image \(Y \sim P_Y\)

Transform and quantize: \(X = f(Y)\)

Inverse transform to reconstruct: \(\hat{Y} = g(X)\)

What can we say about \(P_{X \mid Y}\)? Could we control it?

2.3. Relative Entropy Coding/Channel Simulation

Correlated r.v.s \(X, Y \sim P_{X, Y}\)

Alice receives \(Y \sim P_Y\)

Bob wants to simulate \(X \sim P_{X \mid Y}\)

How many bits does Alice need to send to Bob?

2.4. Relative Entropy Coding/Channel Simulation

How many bits does Alice need to send to Bob?

When common randomness \(S\) available: \[ H[X \mid S] \leq I[X; Y] + \log (I[X; Y] + 1) + 4. \]

\(H[X]\) - Amount of information in \(P_X\)

\(I[X; Y]\) - Information in \(P_{X, Y}\) compared to \(P_X \otimes P_Y\)

\(I[X; Y]\) can be finite even when \(H[X]\) is infinite!

3. Applications of Relative Entropy Coding

3.1. Lossy Compression with Realism Constraints

  • Theis & Agustsson (2021):
    • REC provably better than quantization.
  • Theis et al. (2022):

3.2. Model Compression

Image from Blundell et al. (2015)

3.3. Model Compression

Havasi et al. (2018): MIRACLE

3.4. Data Compression with INRs

Image from Dupont et al. (2021)

Problem: Post-training quantization severely impacts performance!

3.5. Compress variational INRs!

COMBINER: COMpression with Bayesian Implicit Neural Representations

4. Current limitations of REC

Current REC algorithms are:

  • Too slow (Agustsson & Theis, 2020):
    • Average runtime of any general REC algorithm must scale at least \(2^{I[X; Z]}\)
  • Too limited:
    • Uniforms only (Agustsson & Theis, 2020)
    • 1D unimodal distributions only (F et al., 2022)
  • Too much codelength overhead

Open problem: \(\mathcal{O}(I[X; Z])\) runtime when both \(P_{Z \mid X}\) and \(P_Z\) are multivariate Gaussian?

5. Take home message: Overview and Applications

  • REC is a stochastic compression framework
  • Alternative to quantization and entropy coding
  • It finds applications in:
    • Lossy compression with realism constraints
    • Model compression
    • Compressing Bayesian INRs
  • Currently still too slow or limited

6. Greedy Poisson Rejection Sampling

6.1. Poisson Processes

  • Collection of random points in space
  • Focus on spatio-temporal processes on \(\mathbb{R}^D \times \mathbb{R}^+\)
  • Exponential inter-arrival times
  • Spatial distribution \(P_{X}\)

6.2. Example with \(P_{X} = \mathcal{N}(0, 1)\)

empty_pp.png

6.3. Example with \(P_{X} = \mathcal{N}(0, 1)\)

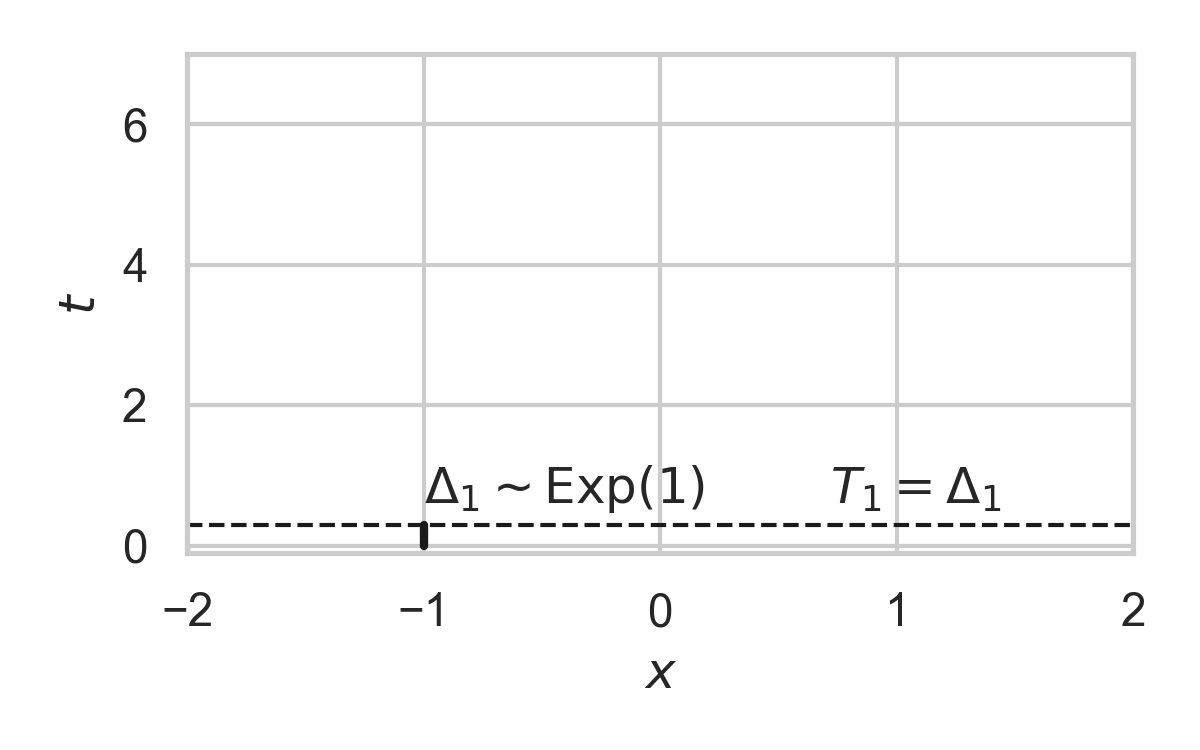
pp_t1.png

6.4. Example with \(P_{X} = \mathcal{N}(0, 1)\)

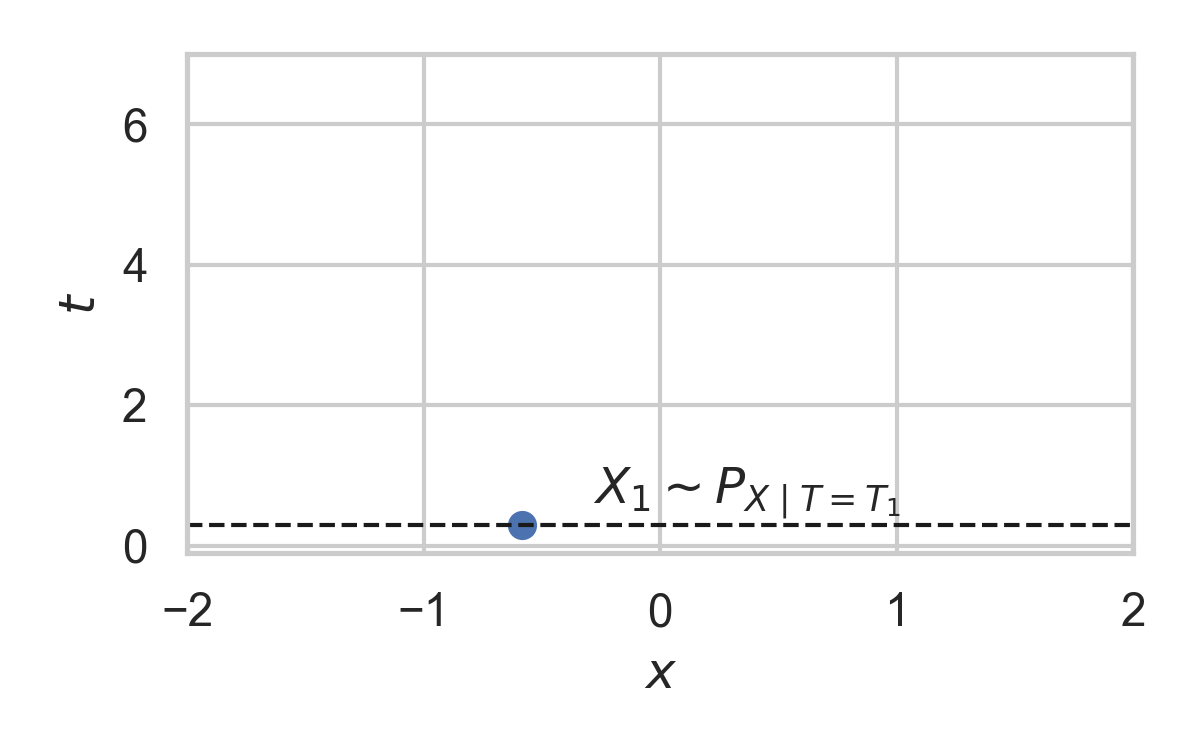
pp_x1.png

6.5. Example with \(P_{X} = \mathcal{N}(0, 1)\)

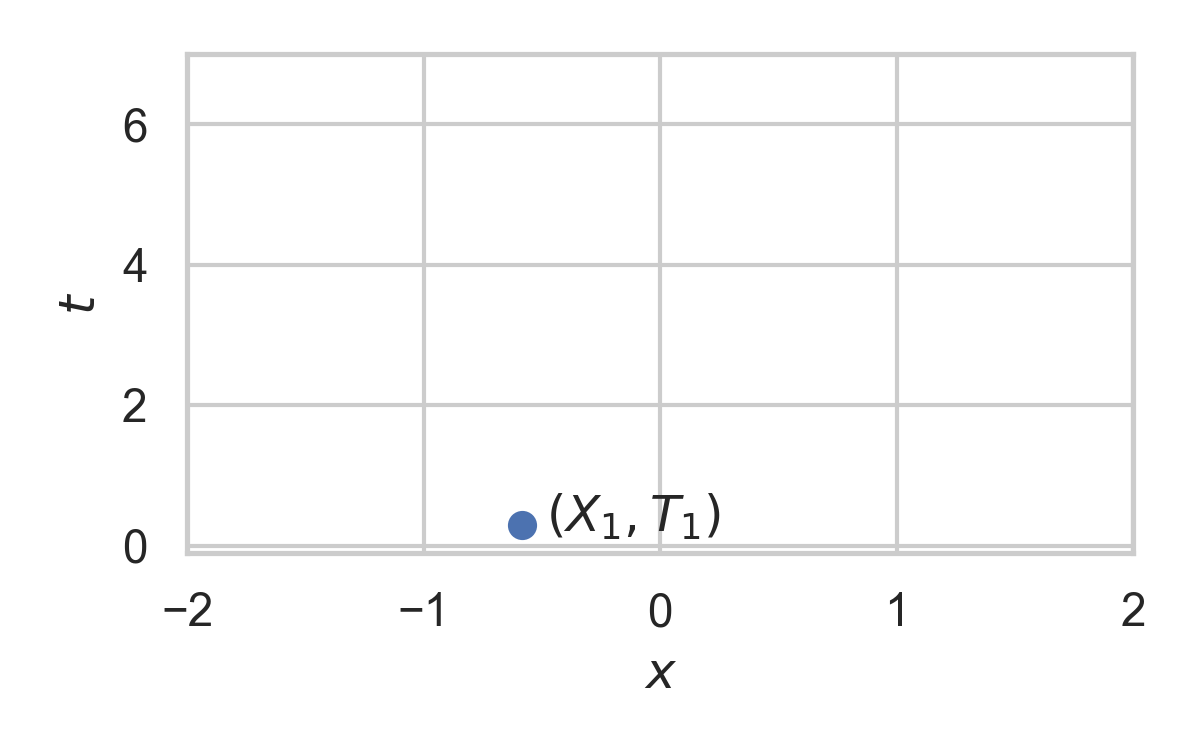
pp_t1_x1.png

6.6. Example with \(P_{X} = \mathcal{N}(0, 1)\)

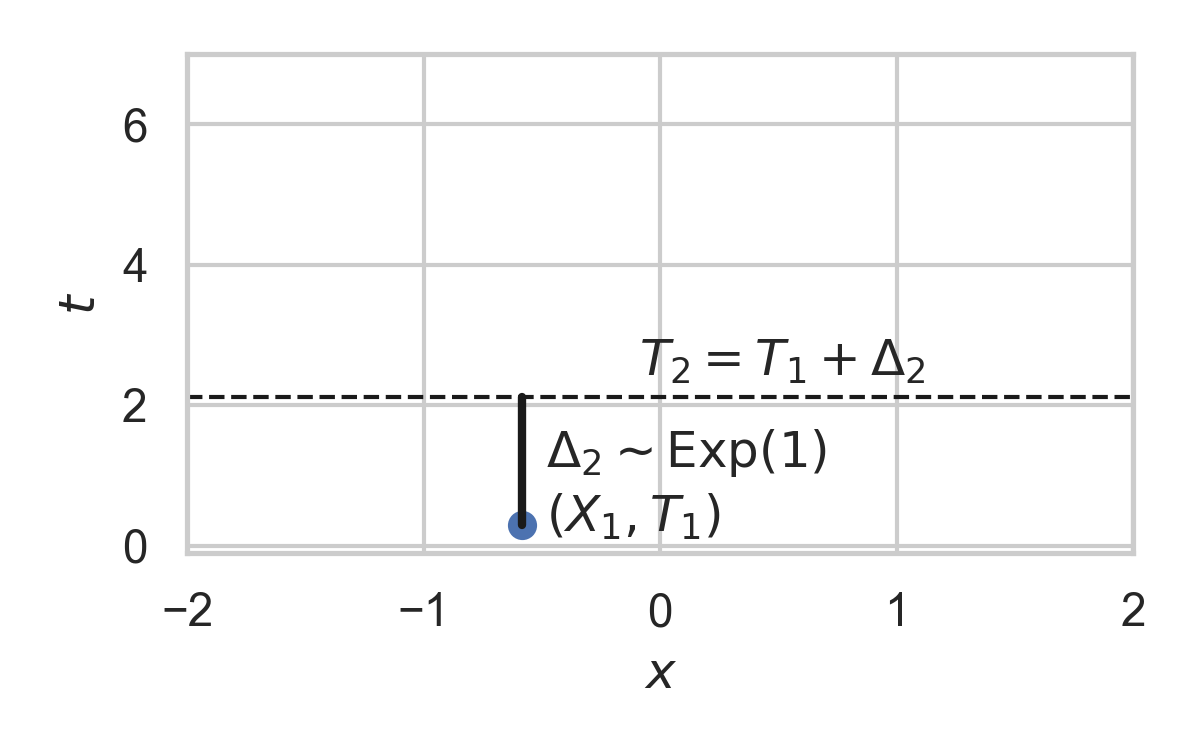
pp_t2.png

6.7. Example with \(P_{X} = \mathcal{N}(0, 1)\)

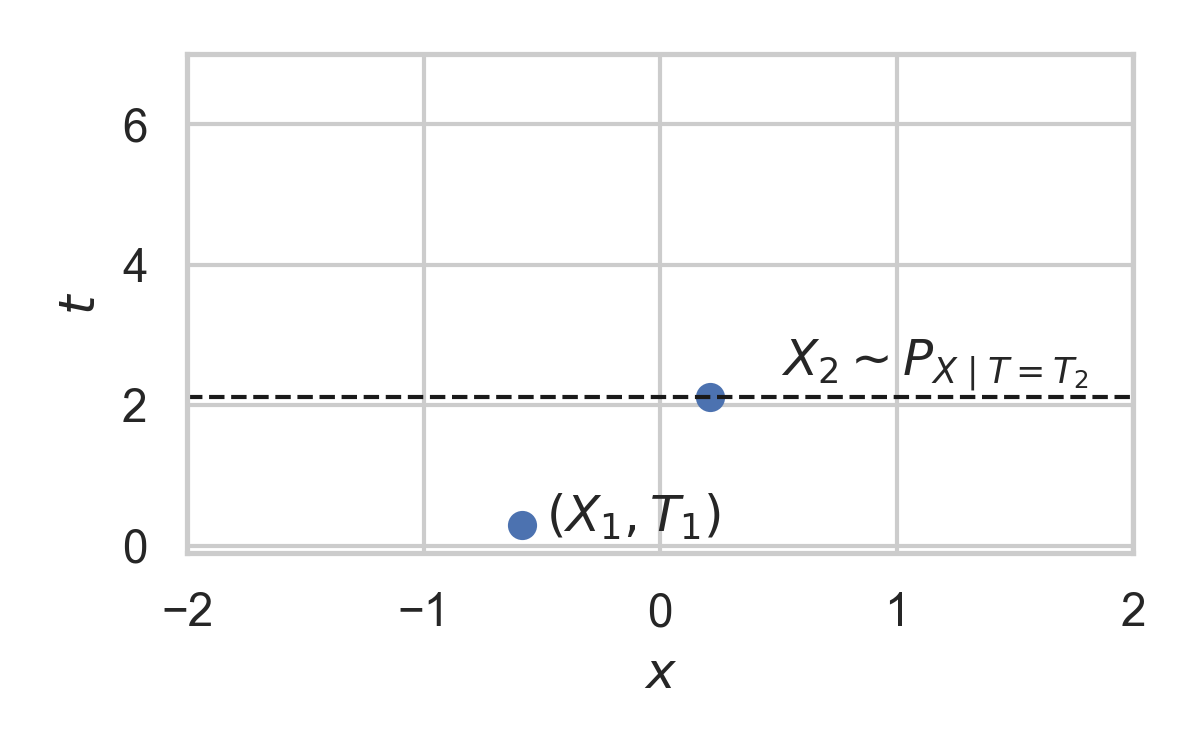
pp_x2.png

6.8. Example with \(P_{X} = \mathcal{N}(0, 1)\)

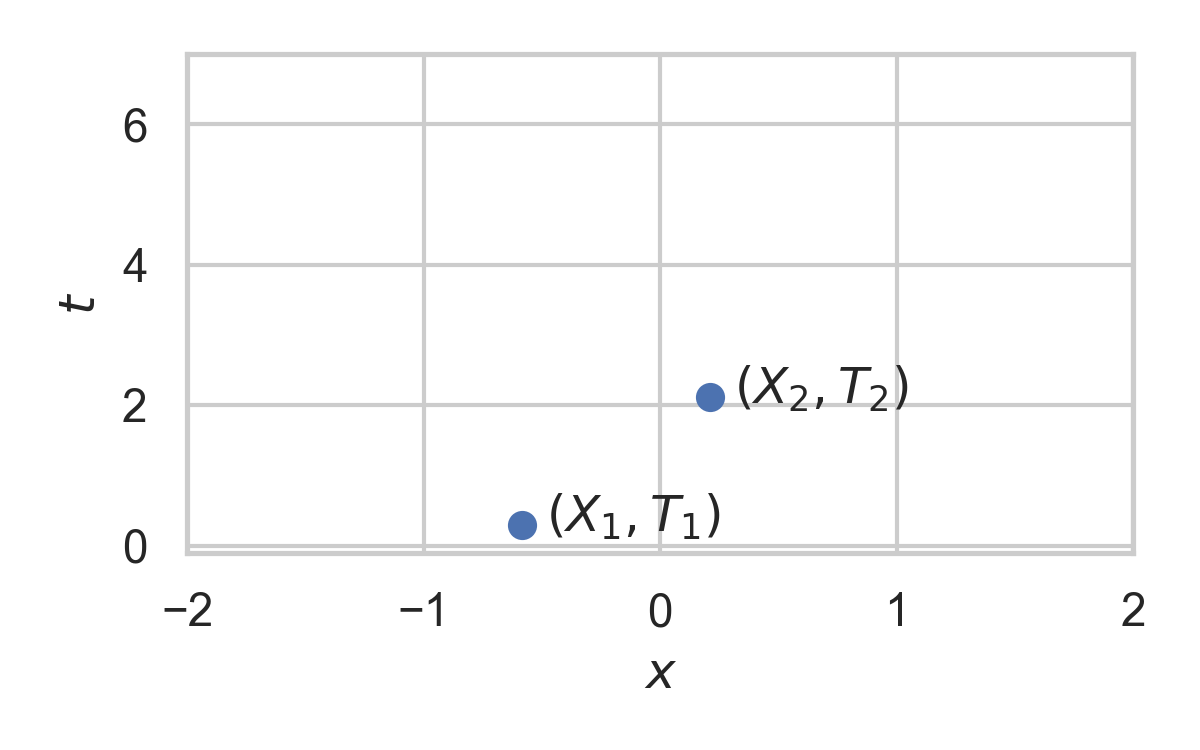
pp_t2_x2.png

6.9. Example with \(P_{X} = \mathcal{N}(0, 1)\)

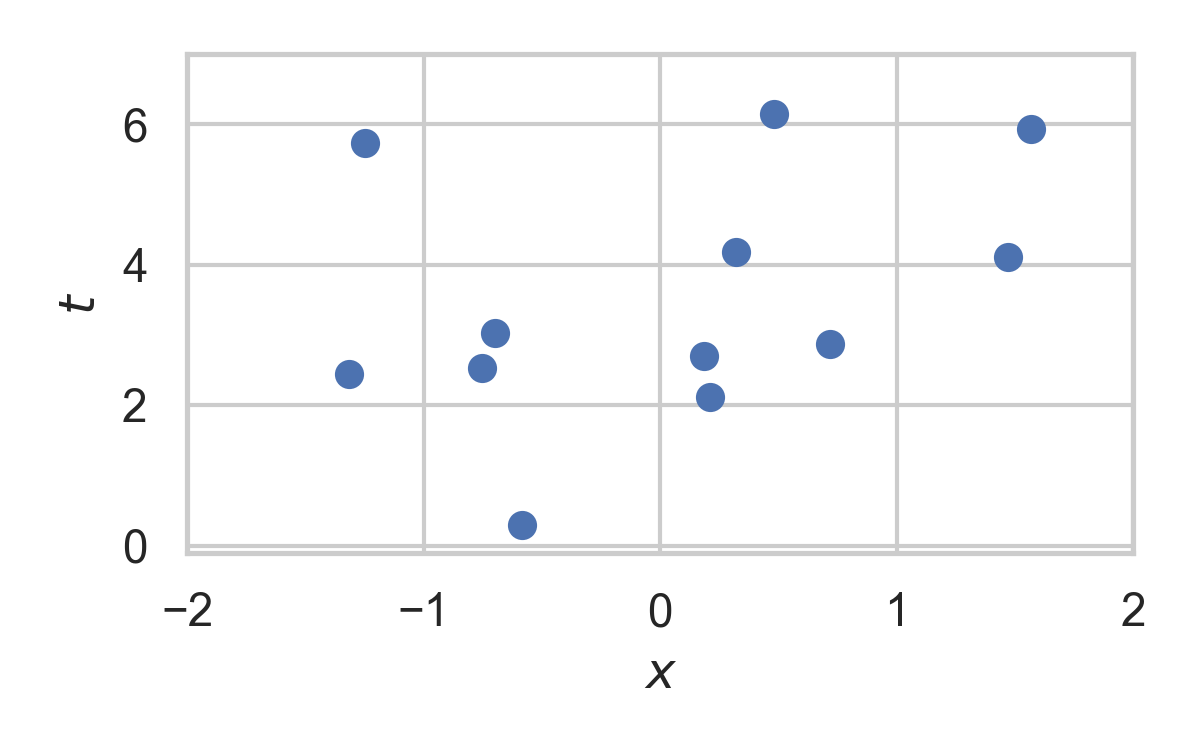
pp_sim.png

6.10. Greedy Poisson Rejection Sampling

6.11. GPRS with \(P_X = \mathcal{N}(0, 1), P_{X \mid Y} = \mathcal{N}(1, 1/16)\)

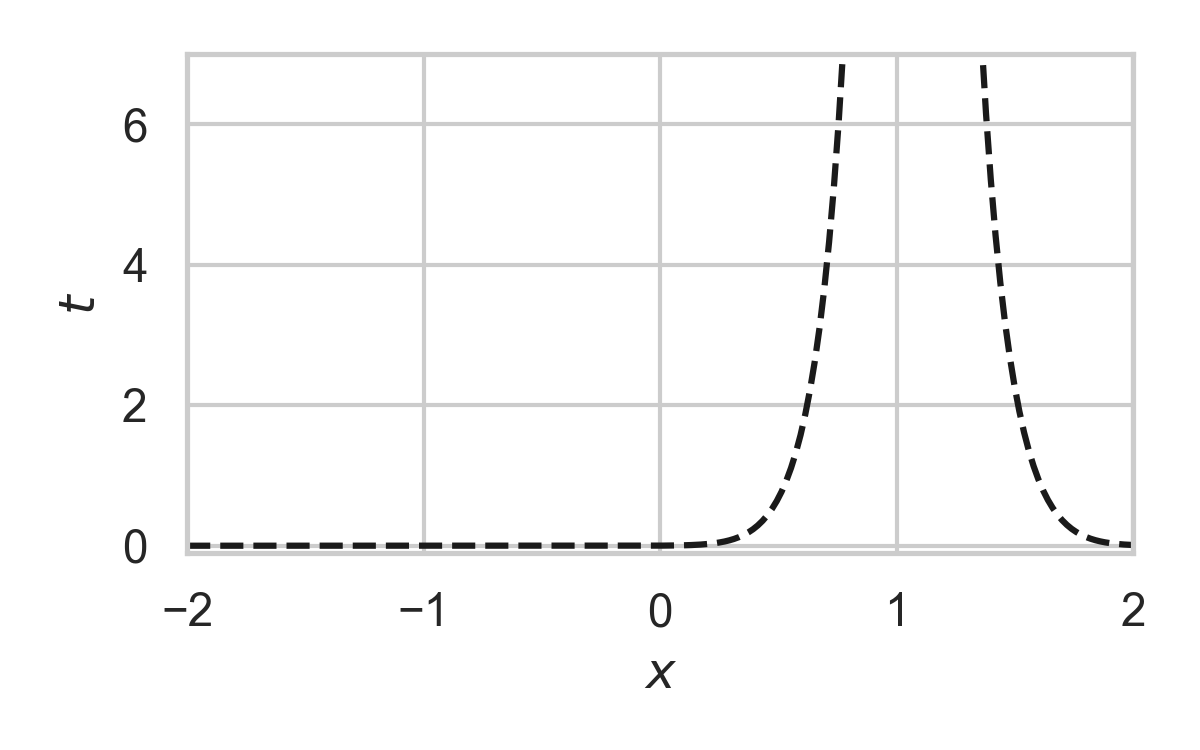
gprs_0.png

6.12. GPRS with \(P_X = \mathcal{N}(0, 1), P_{X \mid Y} = \mathcal{N}(1, 1/16)\)

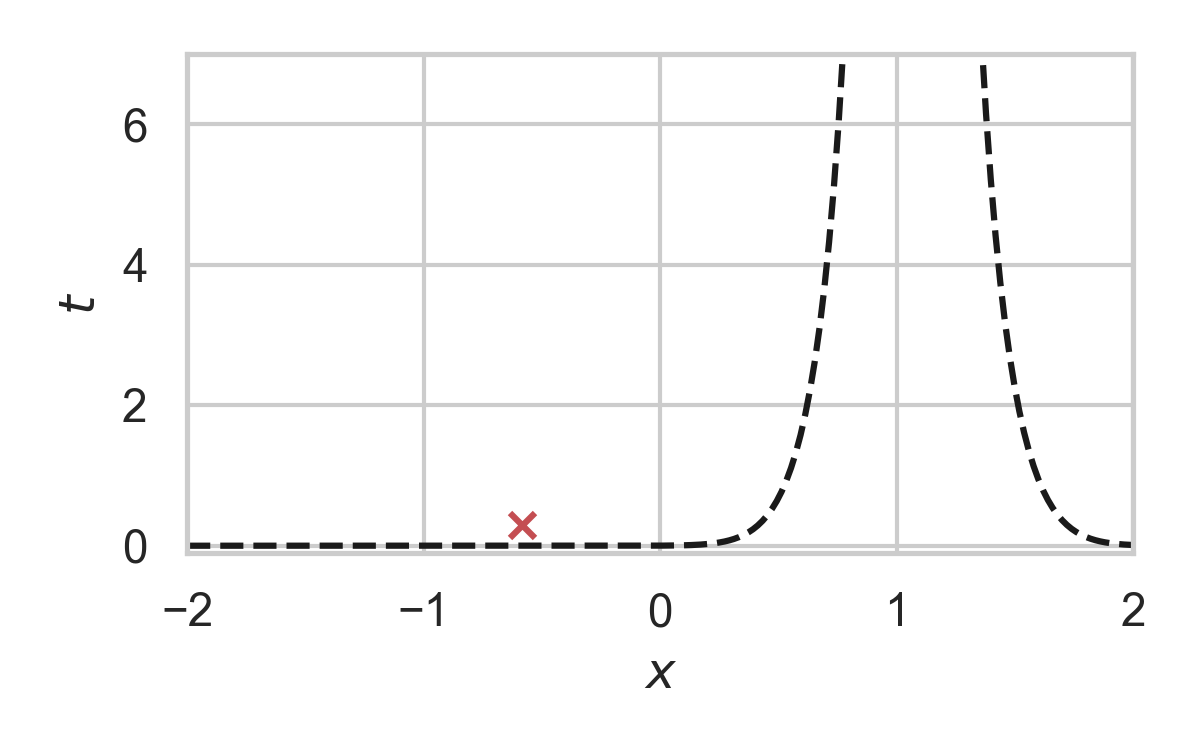
gprs_1.png

6.13. GPRS with \(P_X = \mathcal{N}(0, 1), P_{X \mid Y} = \mathcal{N}(1, 1/16)\)

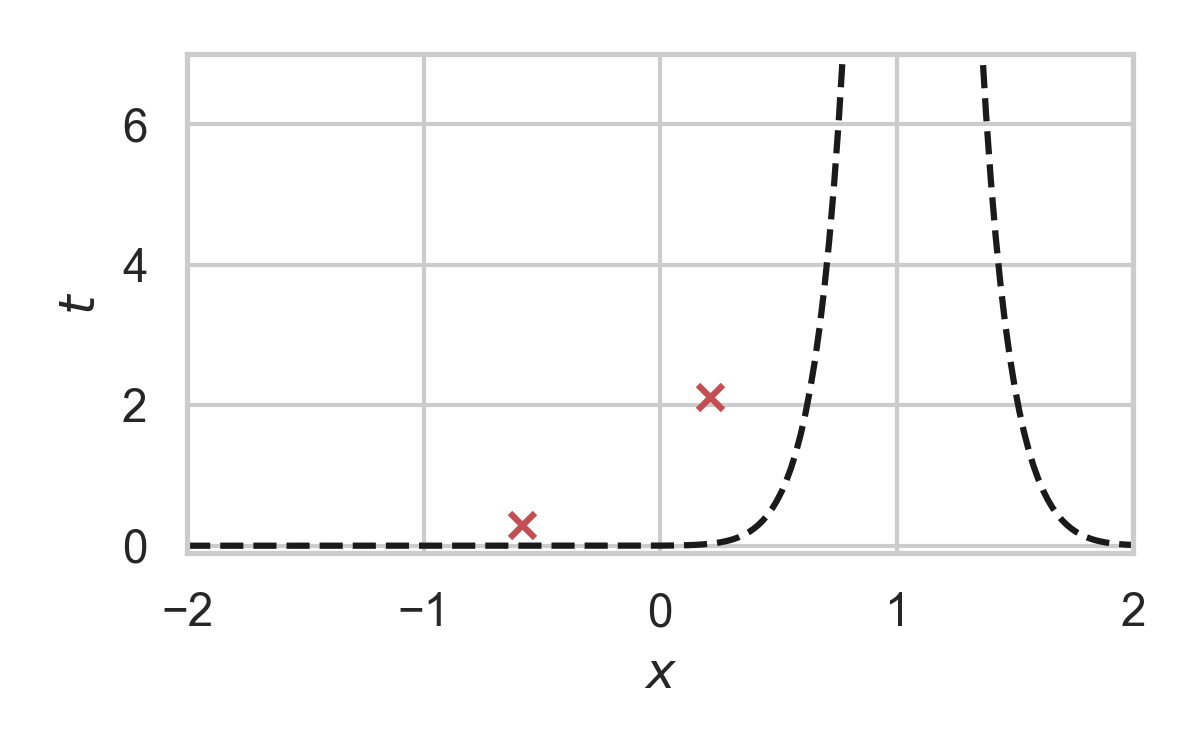
gprs_2.png

6.14. GPRS with \(P_X = \mathcal{N}(0, 1), P_{X \mid Y} = \mathcal{N}(1, 1/16)\)

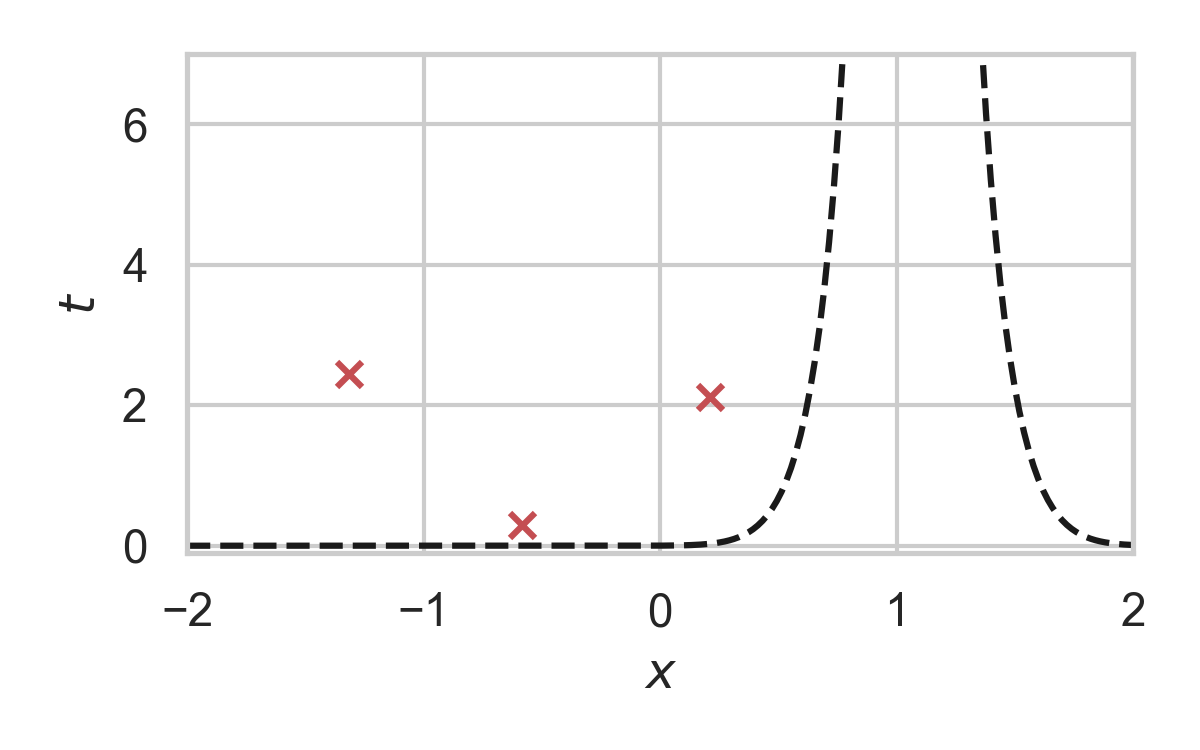
gprs_3.png

6.15. GPRS with \(P_X = \mathcal{N}(0, 1), P_{X \mid Y} = \mathcal{N}(1, 1/16)\)

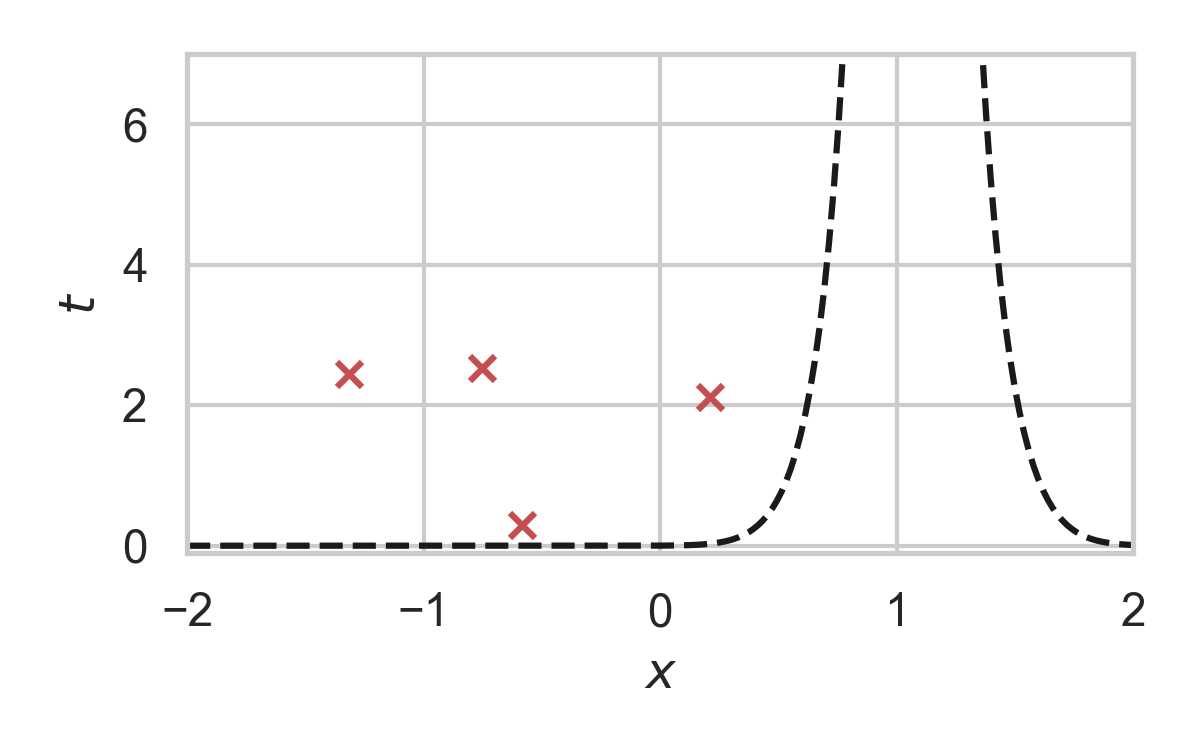
gprs_4.png

6.16. GPRS with \(P_X = \mathcal{N}(0, 1), P_{X \mid Y} = \mathcal{N}(1, 1/16)\)

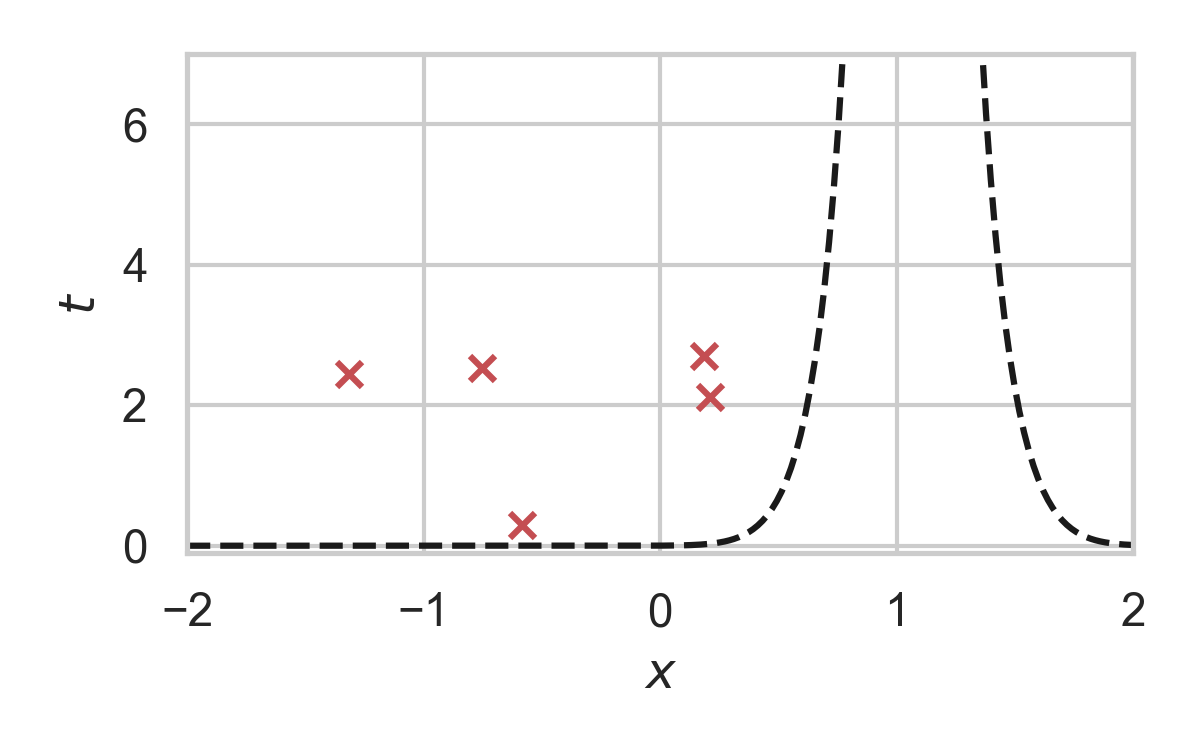
gprs_5.png

6.17. GPRS with \(P_X = \mathcal{N}(0, 1), P_{X \mid Y} = \mathcal{N}(1, 1/16)\)

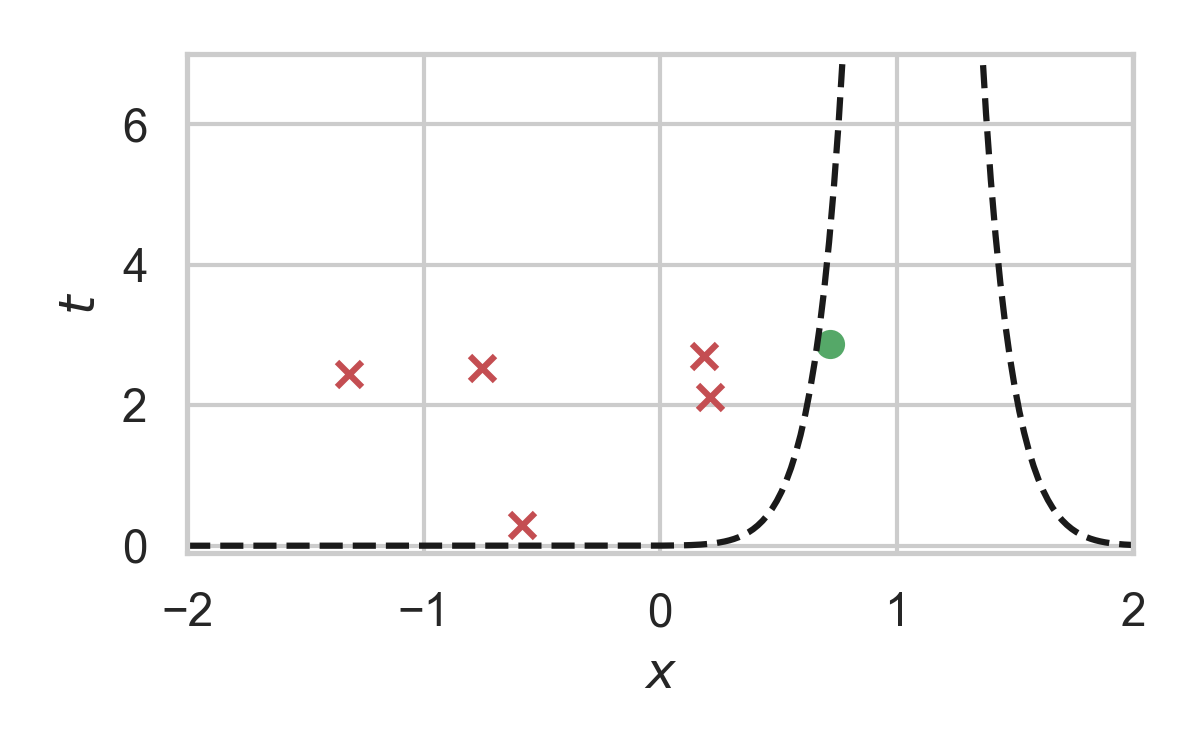
gprs_accept.png

6.18. How to find the function?

\[ \sigma(h) = \int_0^h \frac{1}{w_{X \mid Y}(\eta) - \eta \cdot w_X(\eta)} \, d\eta, \]

where \[ w_X(h) = \mathbb{P}_{Z \sim P_X}\left[\frac{dP_{X \mid Y}}{dP_X}(Z) \geq h \right] \] \[ w_{X \mid Y}(h) = \mathbb{P}_{Z \sim P_{X \mid Y}}\left[\frac{dP_{X \mid Y}}{dP_X}(Z) \geq h \right] \]

6.19. Analysis of GPRS

Codelength

\begin{align} H[X \mid S] &\leq I[X; Y] + \log (I[X; Y] + 1) \\ &\quad + 2 + \frac{1}{1 + I[X; Y] \cdot \ln 2} \end{align}

Runtime

\[ \mathbb{E}[K \mid Y] = \exp(D_{\inf}[P_{X \mid Y} \Vert P_X]) \]

6.20. Speeding up GPRS

gprs_accept.png

6.21. Fast GPRS with \(P_X = \mathcal{N}(0, 1), P_{X \mid Y} = \mathcal{N}(1, 1/16)\)

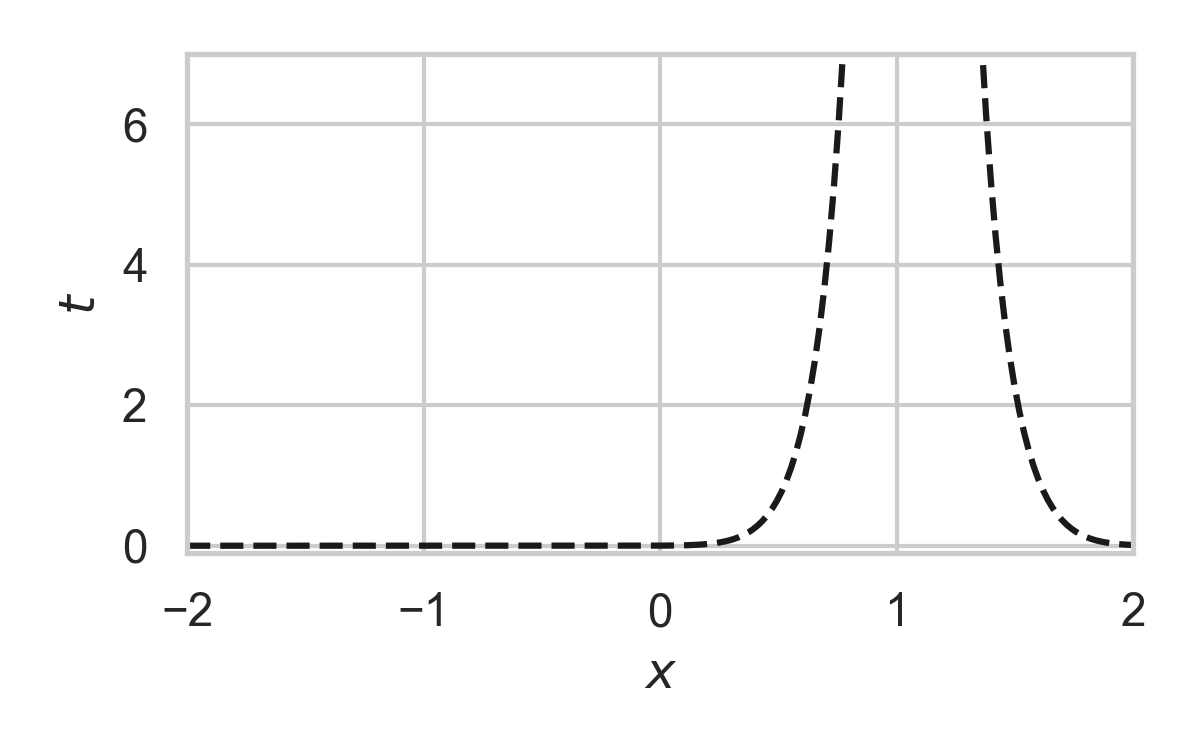
fast_gprs_0.png

6.22. Fast GPRS with \(P_X = \mathcal{N}(0, 1), P_{X \mid Y} = \mathcal{N}(1, 1/16)\)

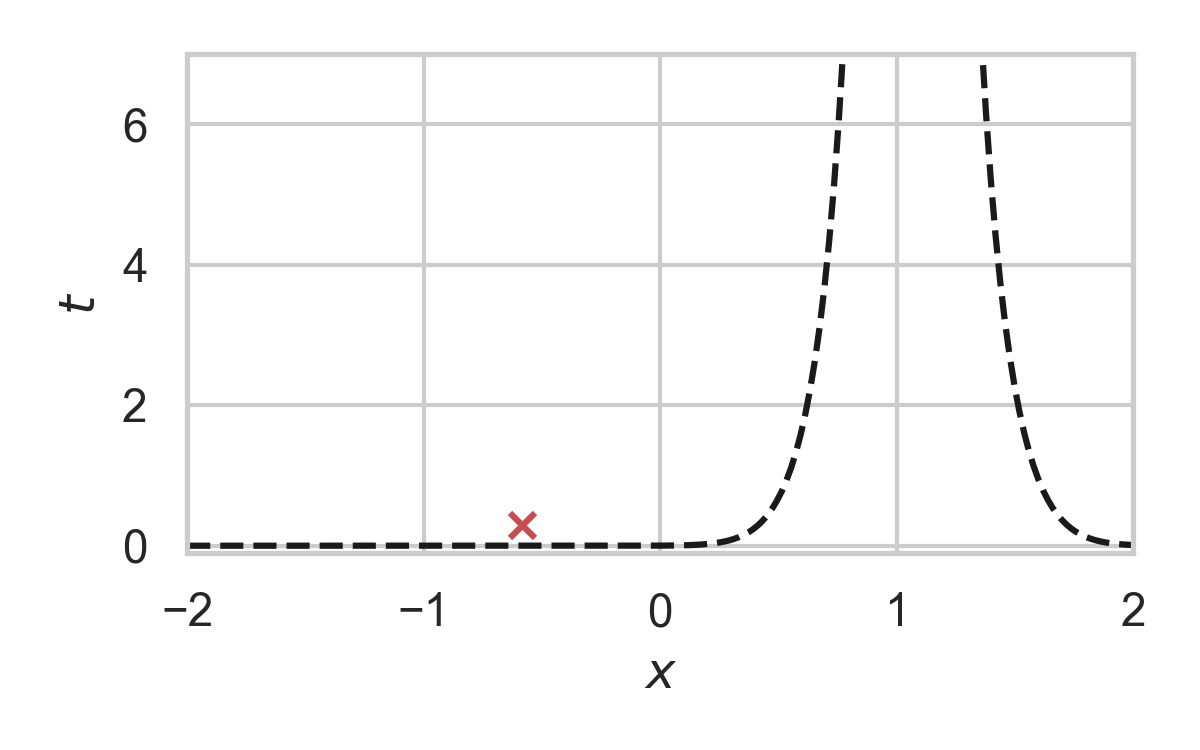
fast_gprs_1.png

6.23. Fast GPRS with \(P_X = \mathcal{N}(0, 1), P_{X \mid Y} = \mathcal{N}(1, 1/16)\)

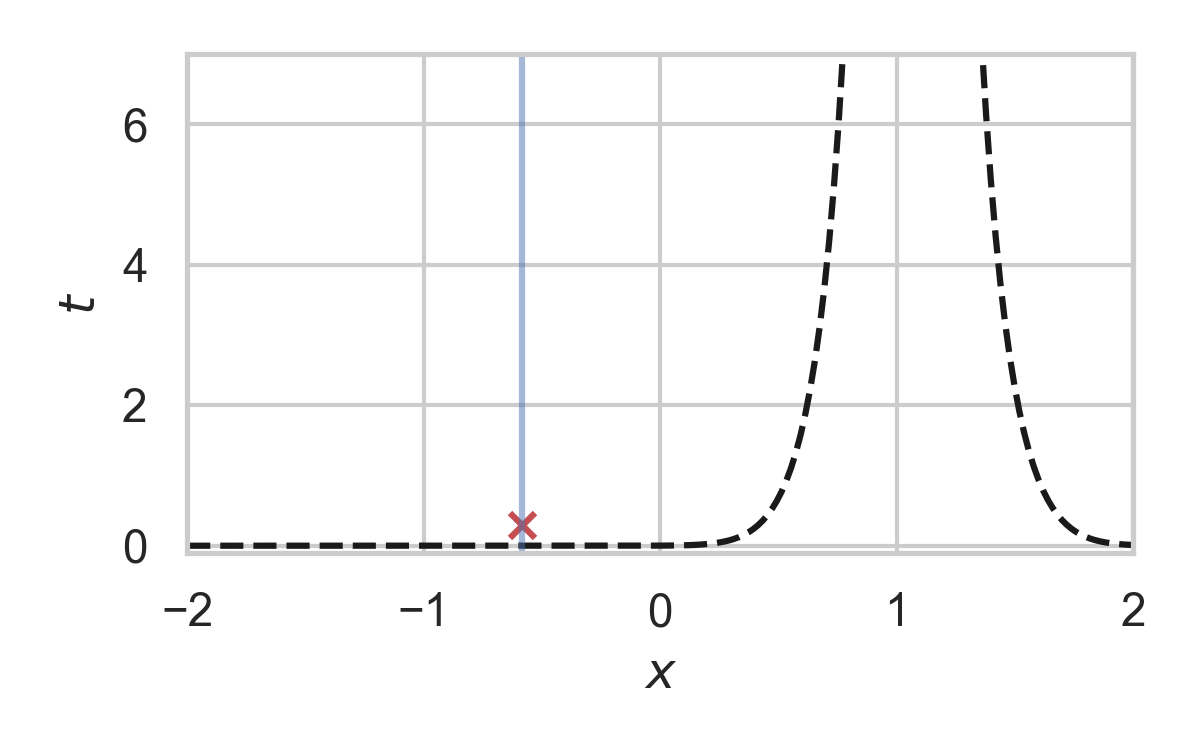
fast_gprs_2.png

6.24. Fast GPRS with \(P_X = \mathcal{N}(0, 1), P_{X \mid Y} = \mathcal{N}(1, 1/16)\)

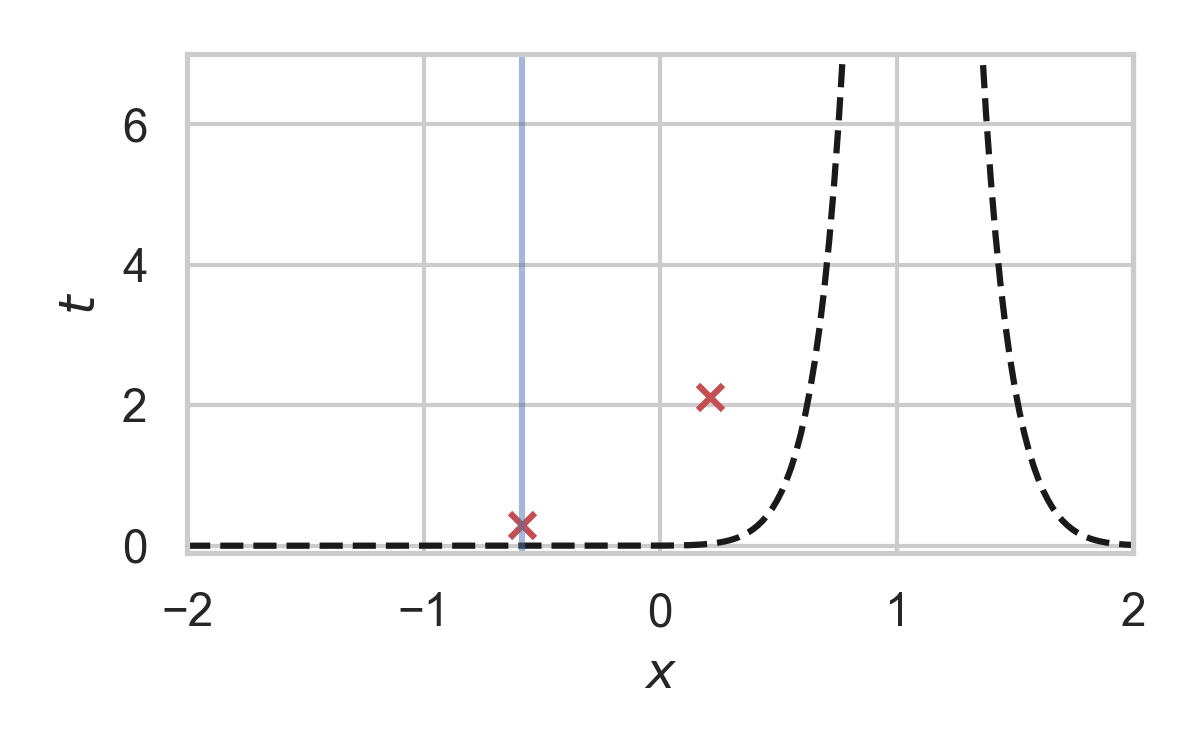
fast_gprs_3.png

6.25. Fast GPRS with \(P_X = \mathcal{N}(0, 1), P_{X \mid Y} = \mathcal{N}(1, 1/16)\)

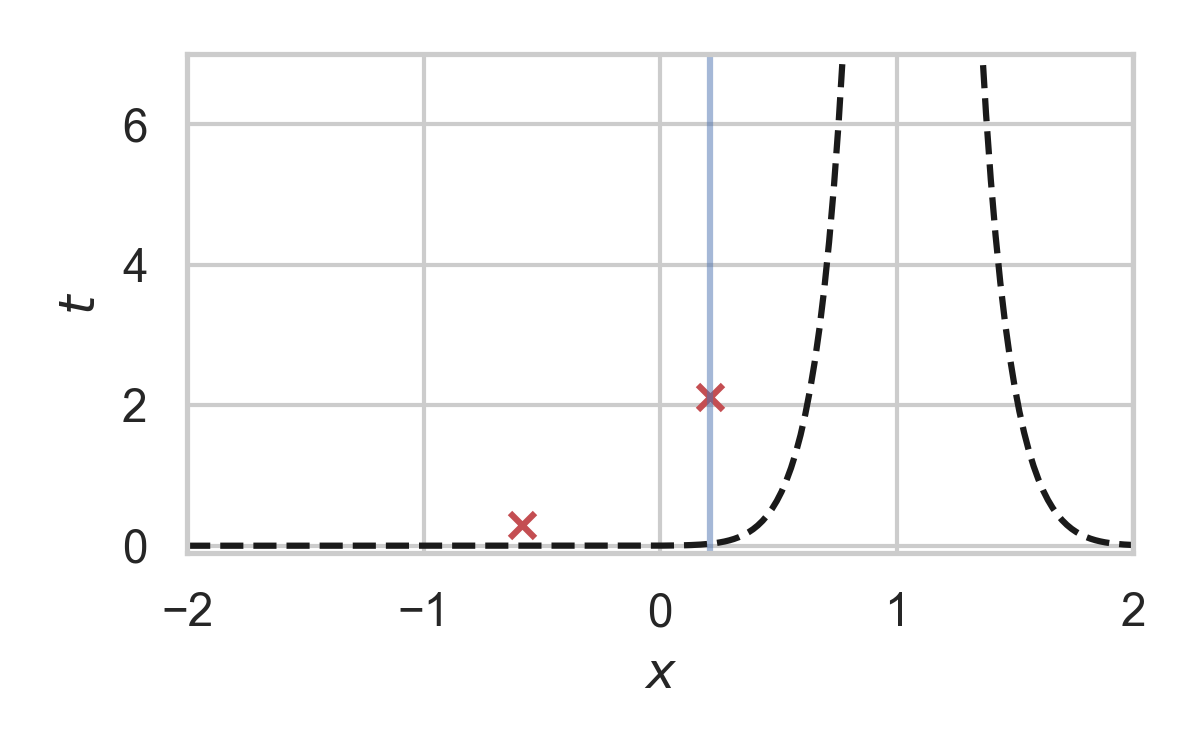
fast_gprs_4.png

6.26. Fast GPRS with \(P_X = \mathcal{N}(0, 1), P_{X \mid Y} = \mathcal{N}(1, 1/16)\)

fast_gprs_5.png

6.27. Analysis of faster GPRS

Now, encode search path \(\pi\).

\(H[\pi] \leq I[X; Z] + \log(I[X; Z] + 1) + \mathcal{O}(1)\)

\(\mathbb{E}[\lvert\pi\rvert] = \mathcal{O}(I[X; Z])\)

7. References

7.1. References I

  • E. Agustsson and L. Theis. "Universally quantized neural compression" In NeurIPS 2020.
  • C. Blundell, J. Cornebise, K. Kavukcuoglu and D. Wierstra. Weight uncertainty in neural network. In ICML 2015.
  • E. Dupont, A. Golinski, M. Alizadeh, Y. W. Teh and Arnaud Doucet. "COIN: compression with implicit neural representations" arXiv preprint arXiv:2103.03123, 2021.

7.2. References II

  • G. F. “Greedy Poisson Rejection Sampling” NeurIPS 2023, to appear.
  • G. F.*, S. Markou*, and J. M. Hernandez-Lobato. "Fast relative entropy coding with A* coding". In ICML 2022.
  • D. Goc and G. F. “On Channel Simulation Conjectures” unpublished.

7.3. References III

  • Z. Guo*, G. F.*, J. He, Z. Chen and J. M. Hernandez Lobato, “Compression with Bayesian Implicit Neural Representations” NeurIPS 2023, to appear.
  • P. Harsha, R. Jain, D. McAllester, and J. Radhakrishnan, “The communication complexity of correlation,” IEEE Transactions on Information Theory, vol. 56, no. 1, pp. 438–449, 2010.
  • M. Havasi, R. Peharz, and J. M. Hernández-Lobato. "Minimal Random Code Learning: Getting Bits Back from Compressed Model Parameters" In ICLR 2019.

7.4. References IV

  • J. He*, G. F.*, Z. Guo and J. M. Hernandez Lobato, “RECOMBINER: Robust and Enhanced Compression with Bayesian Implicit Neural Representations” unpublished.
  • C. T. Li and A. El Gamal, “Strong functional representation lemma and applications to coding theorems,” IEEE Transactions on Information Theory, vol. 64, no. 11, pp. 6967–6978, 2018.

7.5. References V

  • L. Theis and E. Agustsson. On the advantages of stochastic encoders. arXiv preprint arXiv:2102.09270.
  • L. Theis, T. Salimans, M. D. Hoffman and F. Mentzer (2022). Lossy compression with Gaussian diffusion. arXiv preprint arXiv:2206.08889.