An Introduction to Relative Entropy Coding


Gergely Flamich

18/10/2023

gergely-flamich.github.io

1. Talk Overview

  1. Transform coding & problems with \(\lfloor \cdot \rceil\)
  2. What is REC?
  3. How can we use REC?
  4. An example of a REC algorithm
  5. Some recent results

2. In Collaboration With

3. Motivation

3.1. Example: Lossy Image Compression

transform_encoding.png

transform_decoding.png

3.2. The Setup

Get an image \(Y \sim P_Y\)

\(\mathbb{H}[Y]\) bits is best we can do to compress \(Y\)

  • \(\mathbb{H}[Y]\) might be infinite
  • \(\mathbb{H}[Y]\) finite, but \(P_Y\) complicated

3.3. The Transform

\(X = f(Y)\)

  • Pick \(f\) such that \(P_X\) or \(P_{X \mid Y}\) is "nice"
    • DCT
    • inference network of VAE
  • \(\mathbb{H}[X]\) might still be infinite

3.4. Quantization + Entropy Coding

\(\hat{X} = \lfloor X \rceil\)

\(\mathbb{H}[\hat{X}] < \infty\)

  • \(\lfloor \cdot \rceil\) not differentiable
  • Don't have precise control over \(P_{\hat{X} \mid Y}\)

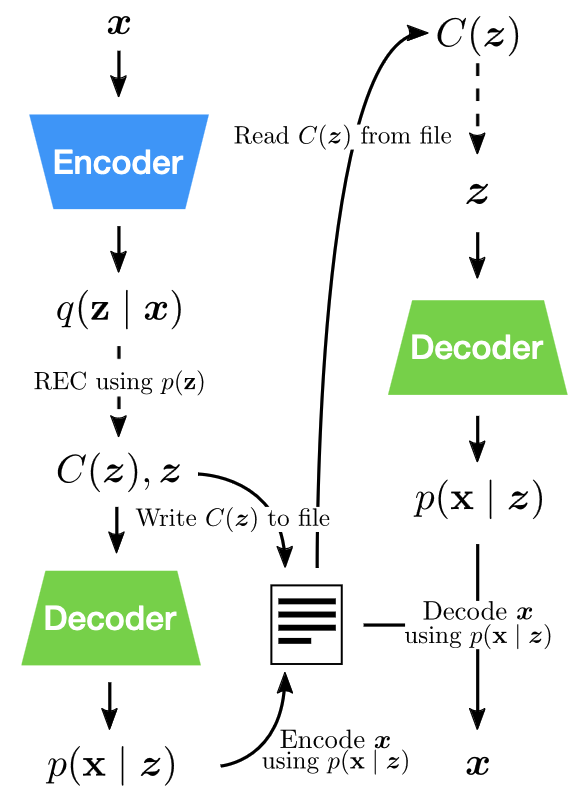
4. What is Relative Entropy Coding?

šŸ’” stochastic alternative to \(\lfloor \cdot \rceil\) & entropy coding

4.1. Relative Entropy Coding

  • \(X = f(Y) + \epsilon\)
  • Encode \(X \sim P_{X \mid Y}\)

Pros:

  • Can use reparameterization trick!
  • Precise control over \(P_{X \mid Y}\) via \(f\) and \(\epsilon\)!

But:

  • How do we encode \(X\)?
  • How many bits do we need?

4.2. Rough Idea for Achievability

Communication problem between Alice and Bob, who:

  • share their PRNG seed \(S\)
  • share \(P_X\) and can easily sample from it

Alice

  1. Simulates \(N\) samples \(X_1, \dots, X_N \sim P_X^{\otimes N}\)
  2. Picks \(K \in [1:N]\) such that \(P_{X_K} \approx P_{X \mid Y}\).
  3. Encodes \(K\) using \(\approx \log K\) bits.

4.3. Coding Efficiency

When common randomness \(S\) available, there exists an algorithm, such that (Li and El Gamal, 2017): \[ {\color{red} I[X; Y]} \leq \mathbb{H}[X \mid S] \leq {\color{red} I[X; Y]} + {\color{blue} \log (I[X; Y] + 1) + 4} \]

\(I[X; Y]\) can be finite even when \(\mathbb{H}[X]\) is infinite!

4.4. Time Complexity

\begin{align} \mathbb{E}[K] &\geq 2^{\mathbb{E}[\log K]} \\ &\geq 2^{\mathbb{H}[X \mid S] - 1} \\ &\geq 2^{I[X; Y] - 1} \\ \end{align}

This is THE limitation of REC in practice currently

5. How Can We Use Relative Entropy Coding?

šŸ’” Think of \(P_{X, Y}\) as a generative model!

5.1. Lossy Compression with Realism Constraints

Rate-Distortion trade-off \[ R(D) = \min_{P_{\hat{Y} \mid Y}} I[Y; \hat{Y}]\,\, \text{s.t.}\,\, \mathbb{E}[\Delta(Y, \hat{Y})] \leq D \]

Rate-Distortion-Perception trade-off

\begin{align} R(D, P) = \min_{P_{\hat{Y} \mid Y}} &\, I[Y; \hat{Y}]\,\, \text{s.t.}\\ \mathbb{E}&[\Delta(Y, \hat{Y})] \leq D \,\,\text{and}\,\, d(P_Y, P_{\hat{Y}}) \leq P \end{align}

5.2. Lossy Compression with Realism Constraints

  • Theis & Agustsson (2021):
    • REC provably better than quantization.
  • Theis et al. (2022):

5.3. Model Compression

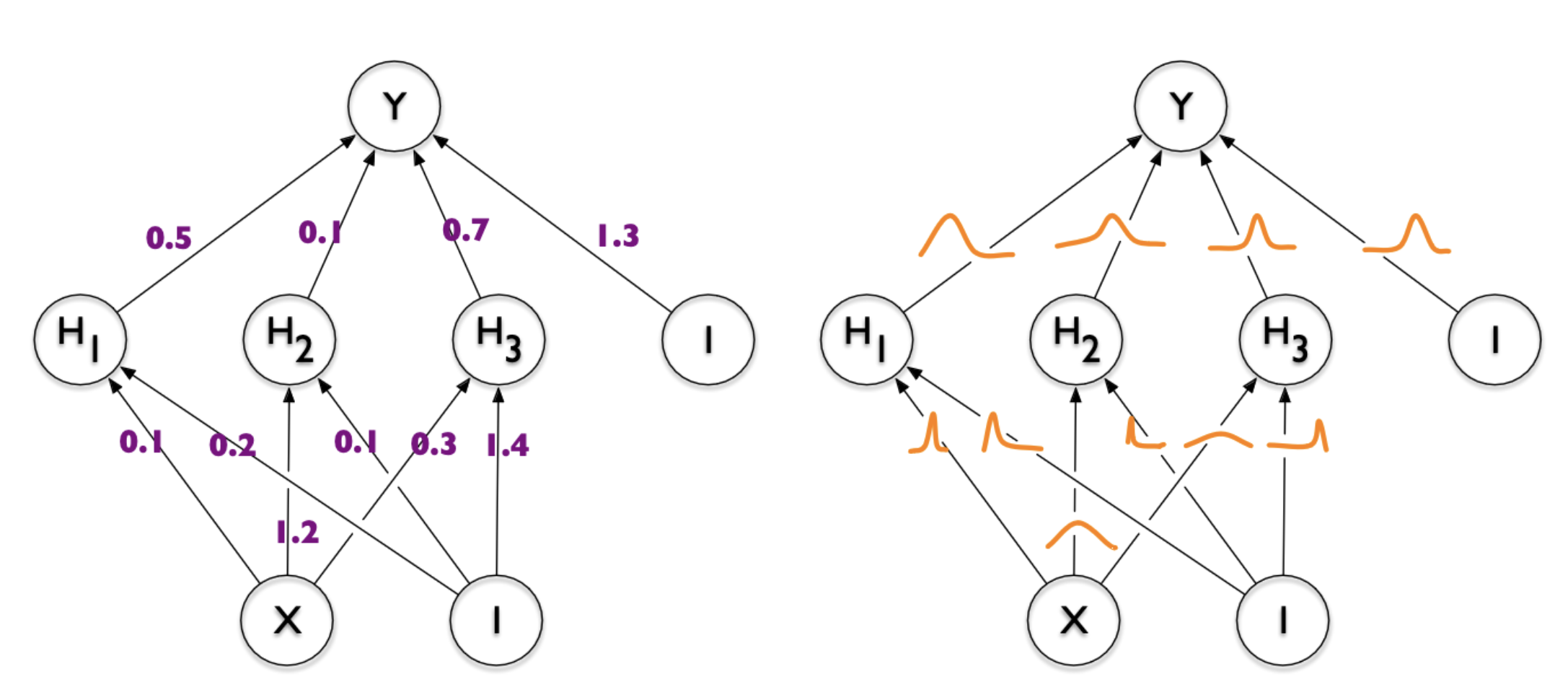
  • Dataset \(\mathcal{D} \sim P_{\mathcal{D}}\)
  • NN \(f(w, x)\) with weights \(w\) with prior \(P_w\)
  • Train weight posterior \(P_{w \mid \mathcal{D}}\) using ELBO
  • Encode \(w \sim P_{w \mid \mathcal{D}}\) in \(I[w; \mathcal{D}]\) bits

Image from Blundell et al. (2015)

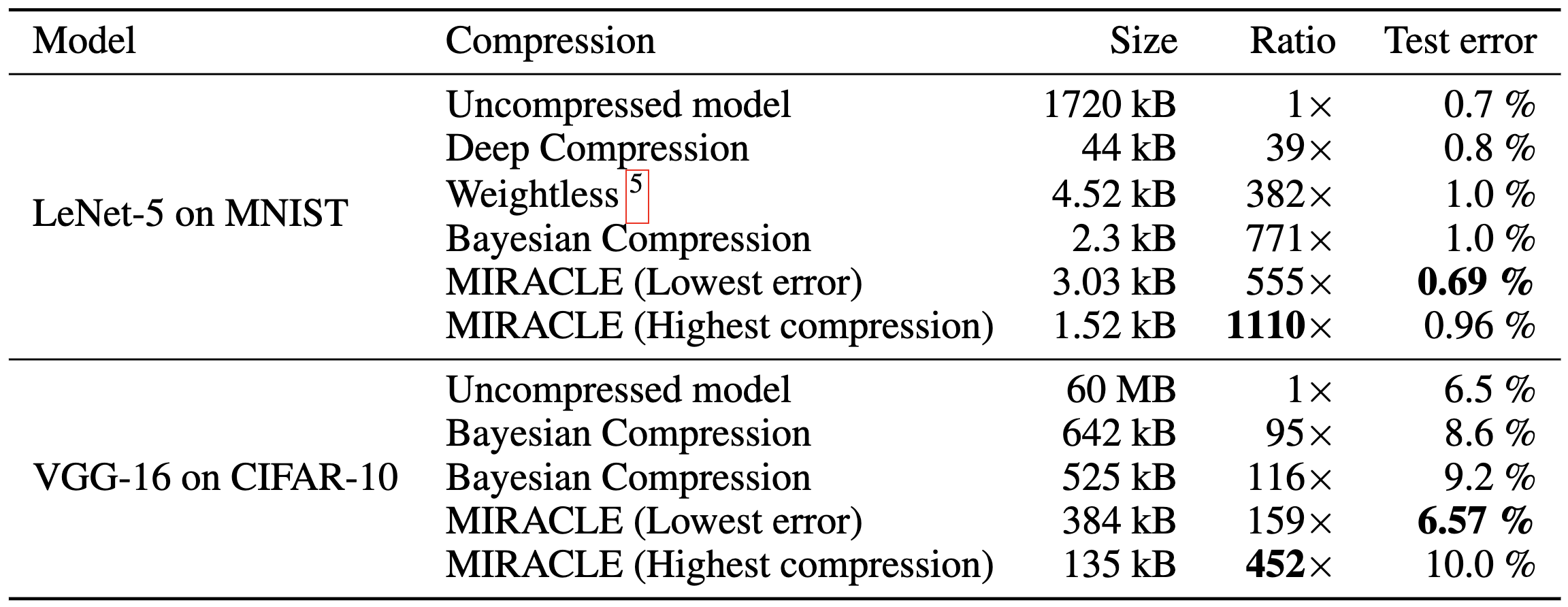
5.4. Model Compression

Havasi et al. (2018): MIRACLE

5.5. Data Compression with INRs

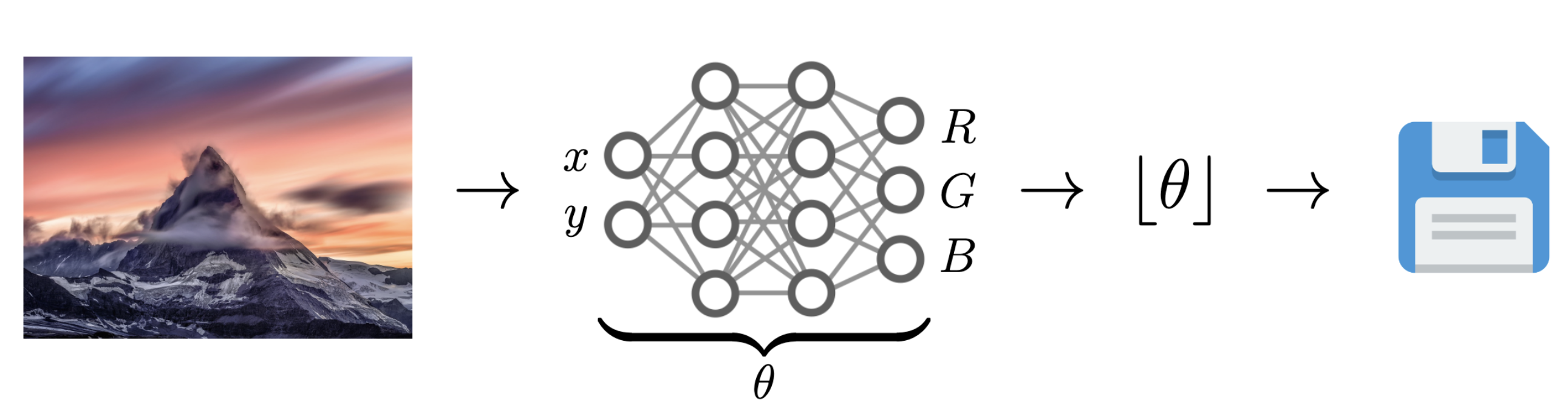
Image from Dupont et al. (2021)

Problem: Post-training quantization severely impacts performance!

5.6. Compress variational INRs!

COMBINER: COMpression with Bayesian Implicit Neural Representations

RECOMBINER: Robust and Enhanced COMBINER

šŸ’”Gradient descent is the transform!

5.7. Compress variational INRs!

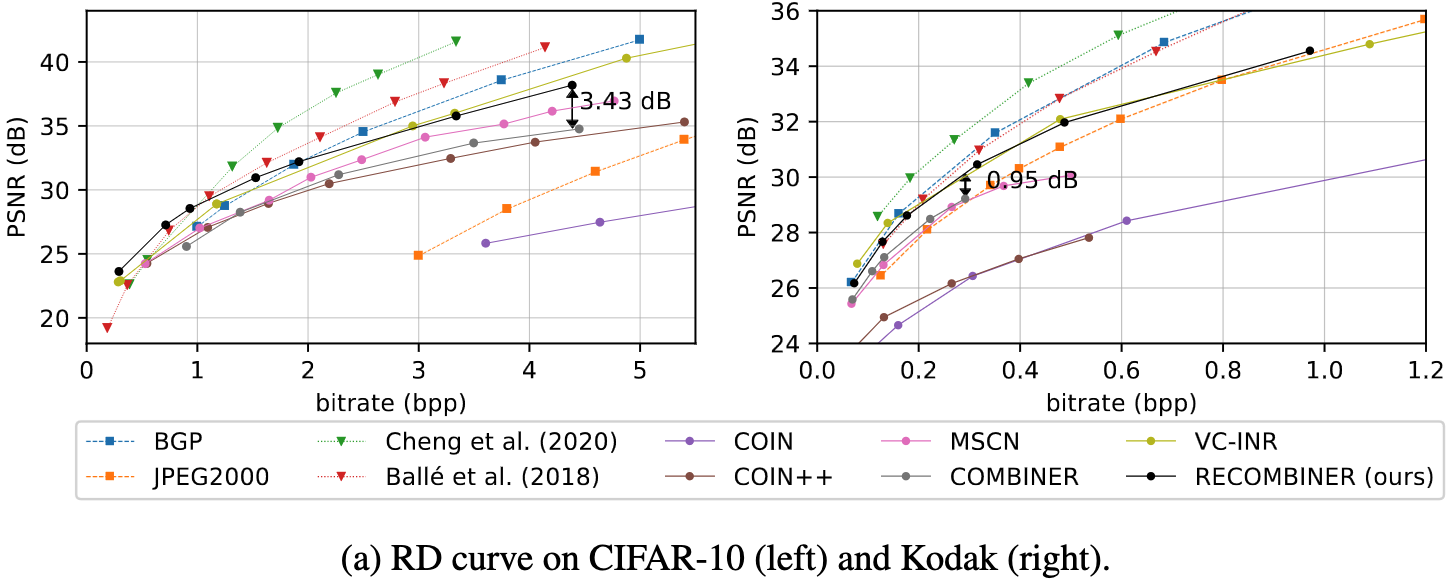
5.8. Compress variational INRs!

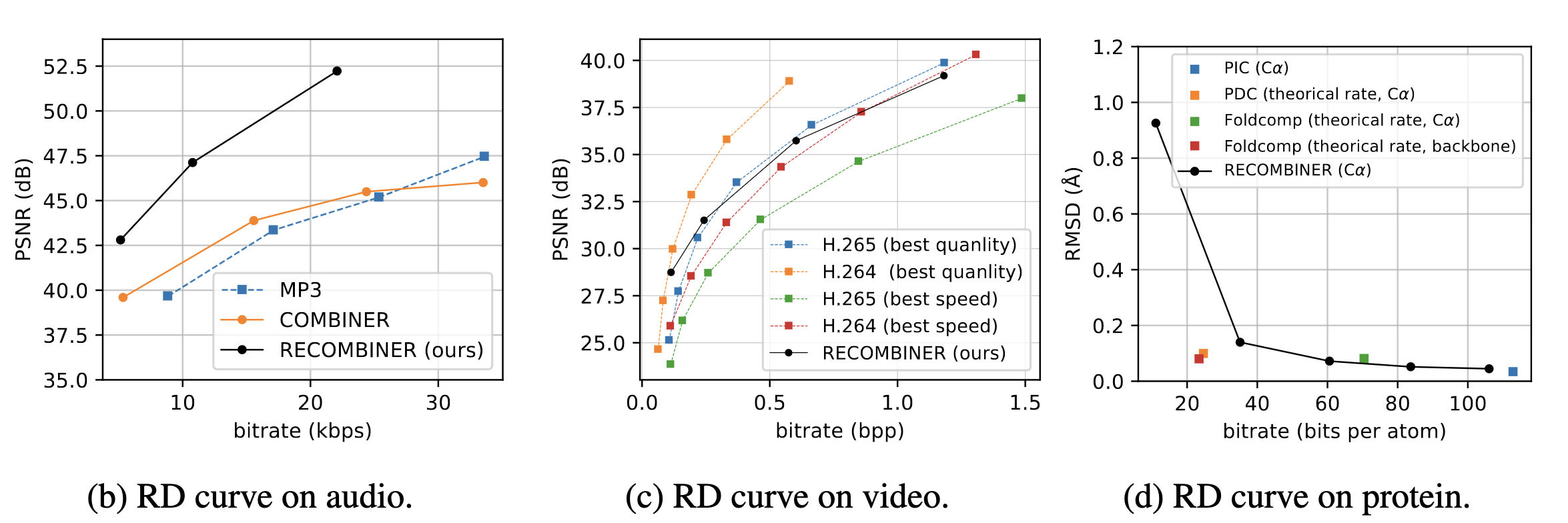
6. Current limitations of REC

  • Too slow (Agustsson & Theis, 2020):
    • Average runtime of any general REC algorithm must scale at least \(2^{I[X; Y]}\)
  • Too limited:
    • Uniforms only (Agustsson & Theis, 2020)
    • 1D unimodal distributions only (F., 2022)
  • Too much codelength overhead

Open problem: \(\mathcal{O}(I[X; Y])\) runtime when both \(P_{Y \mid X}\) and \(P_Y\) are multivariate Gaussian?

7. Take home message: Overview and Applications

  • REC is a stochastic compression framework
  • Alternative to quantization and entropy coding
  • It finds applications in:
    • Lossy compression with realism constraints
    • Model compression
    • Compressing Bayesian INRs
  • Currently still too slow or limited

8. Greedy Poisson Rejection Sampling

8.1. Recap of the Problem

Correlated r.v.s \(X, Y \sim P_{X, Y}\)

Alice receives \(Y \sim P_Y\)

Bob wants to simulate \(X \sim P_{X \mid Y}\)

Share common randomness \(S\)

Shorthand: \(P = P_X\), \(Q = P_{X \mid Y}\)

8.2. Poisson Processes

  • Collection of random points in space
  • Focus on spatio-temporal processes on \(\mathbb{R}^D \times \mathbb{R}^+\)
  • Exponential inter-arrival times
  • Spatial distribution \(P_{X \mid T}\)
  • We will pick it as the common randomness!

8.3. Poisson Processes

8.4. Example with \(P_{X \mid T} = \mathcal{N}(0, 1)\)

empty_pp.png

8.5. Example with \(P_{X \mid T} = \mathcal{N}(0, 1)\)

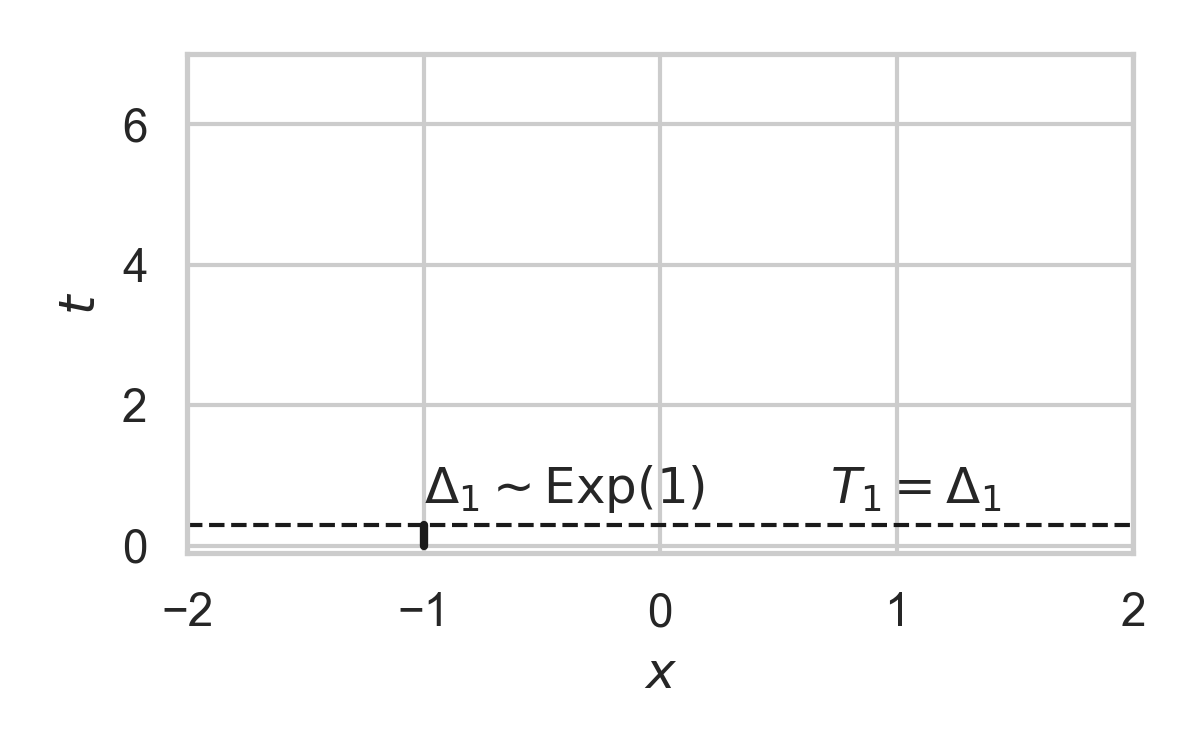
pp_t1.png

8.6. Example with \(P_{X \mid T} = \mathcal{N}(0, 1)\)

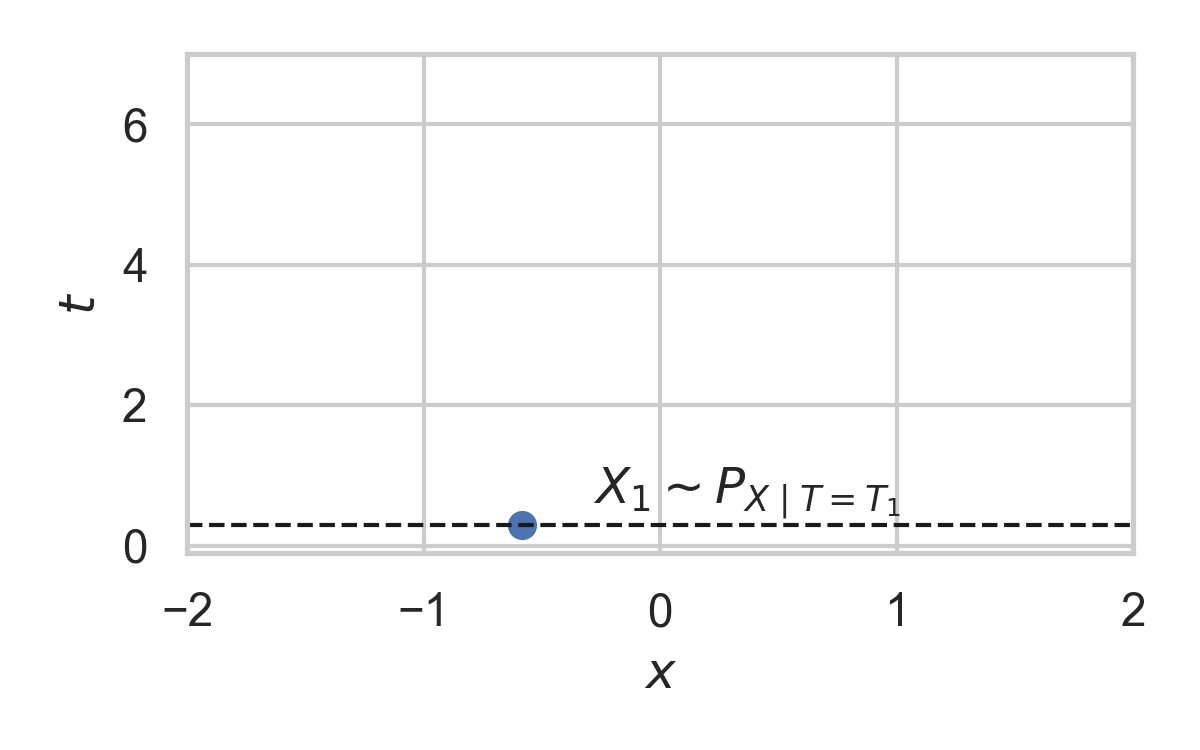
pp_x1.png

8.7. Example with \(P_{X \mid T} = \mathcal{N}(0, 1)\)

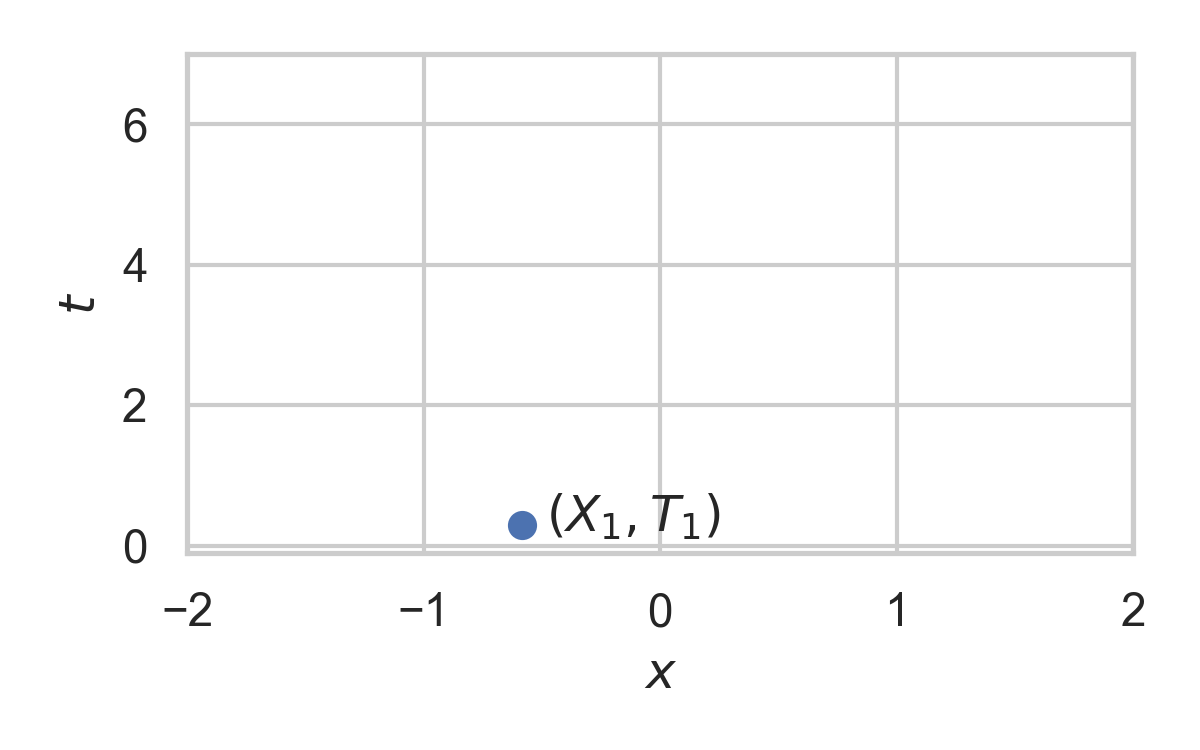
pp_t1_x1.png

8.8. Example with \(P_{X \mid T} = \mathcal{N}(0, 1)\)

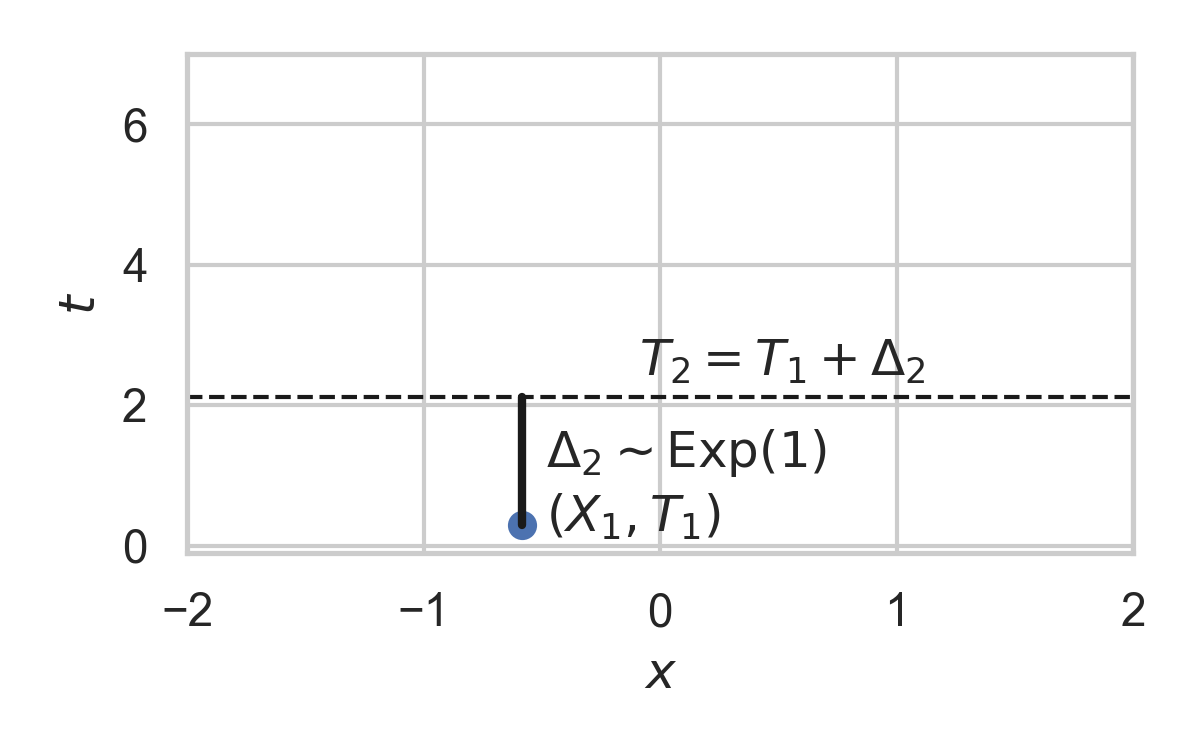
pp_t2.png

8.9. Example with \(P_{X \mid T} = \mathcal{N}(0, 1)\)

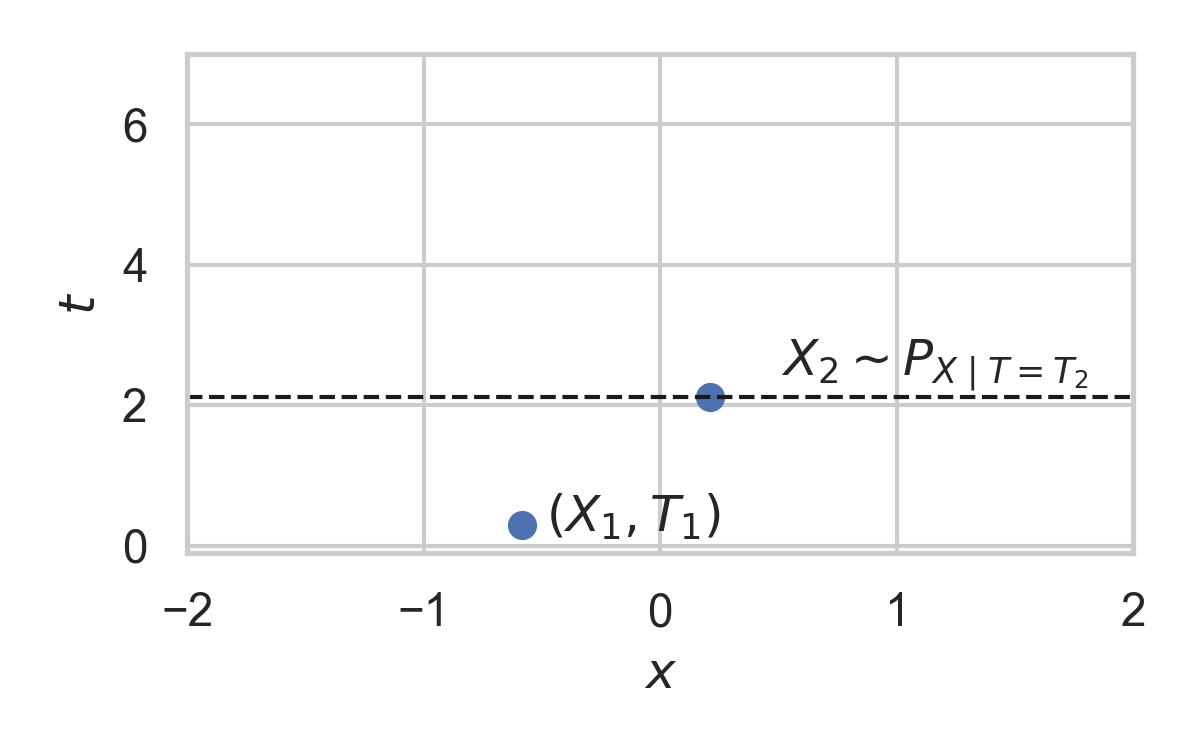
pp_x2.png

8.10. Example with \(P_{X \mid T} = \mathcal{N}(0, 1)\)

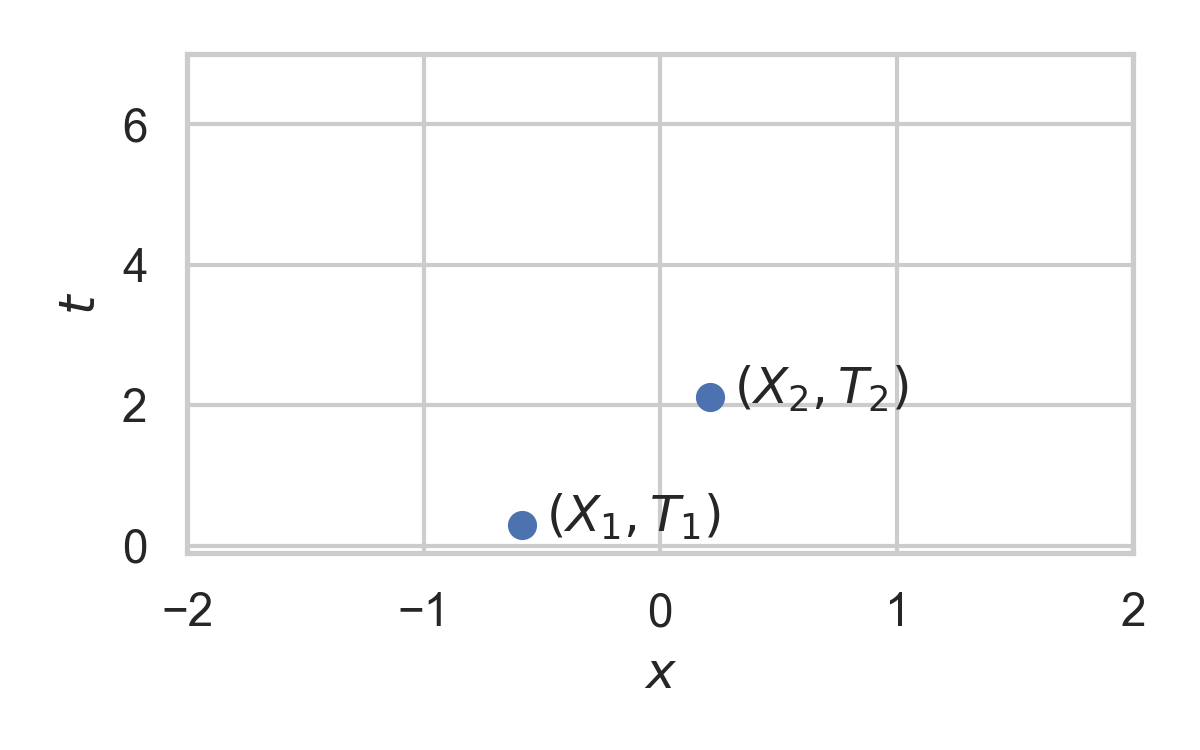
pp_t2_x2.png

8.11. Example with \(P_{X \mid T} = \mathcal{N}(0, 1)\)

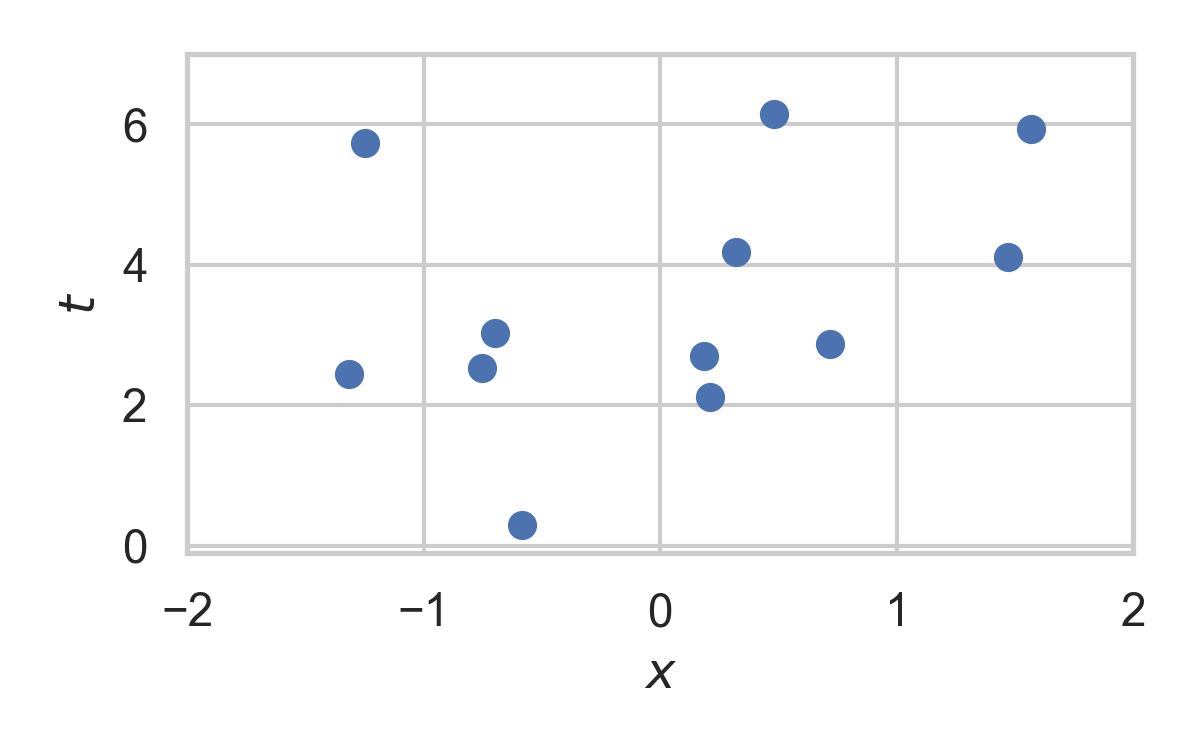
pp_sim.png

8.12. Greedy Poisson Rejection Sampling

šŸ’” Delete some of the points, encode index of the first point that remains

8.13. GPRS with \(P = \mathcal{N}(0, 1), Q = \mathcal{N}(1, 1/16)\)

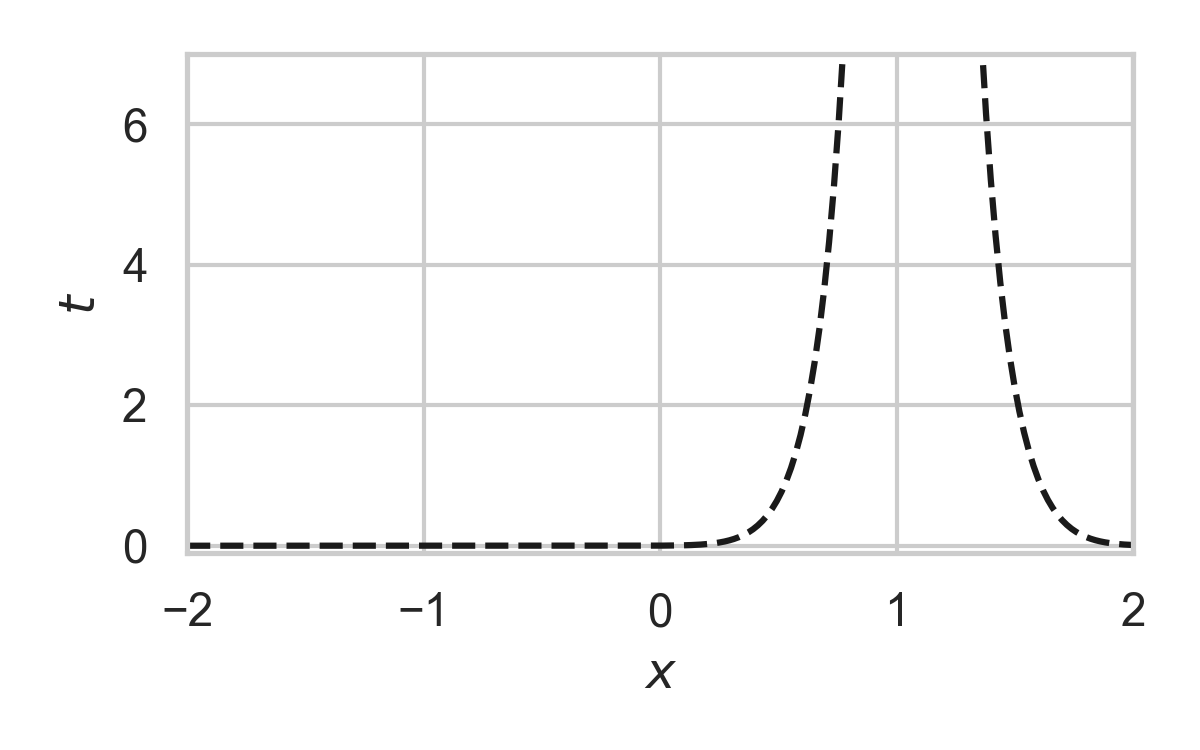
gprs_0.png

8.14. GPRS with \(P = \mathcal{N}(0, 1), Q = \mathcal{N}(1, 1/16)\)

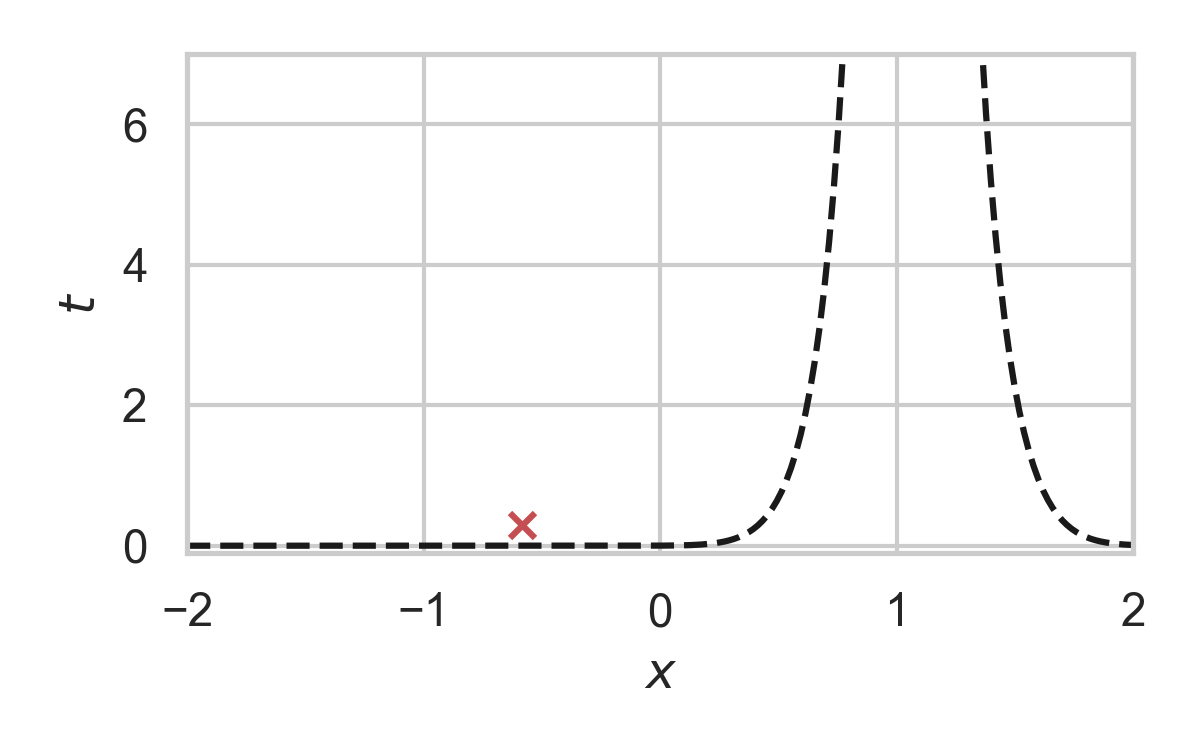
gprs_1.png

8.15. GPRS with \(P = \mathcal{N}(0, 1), Q = \mathcal{N}(1, 1/16)\)

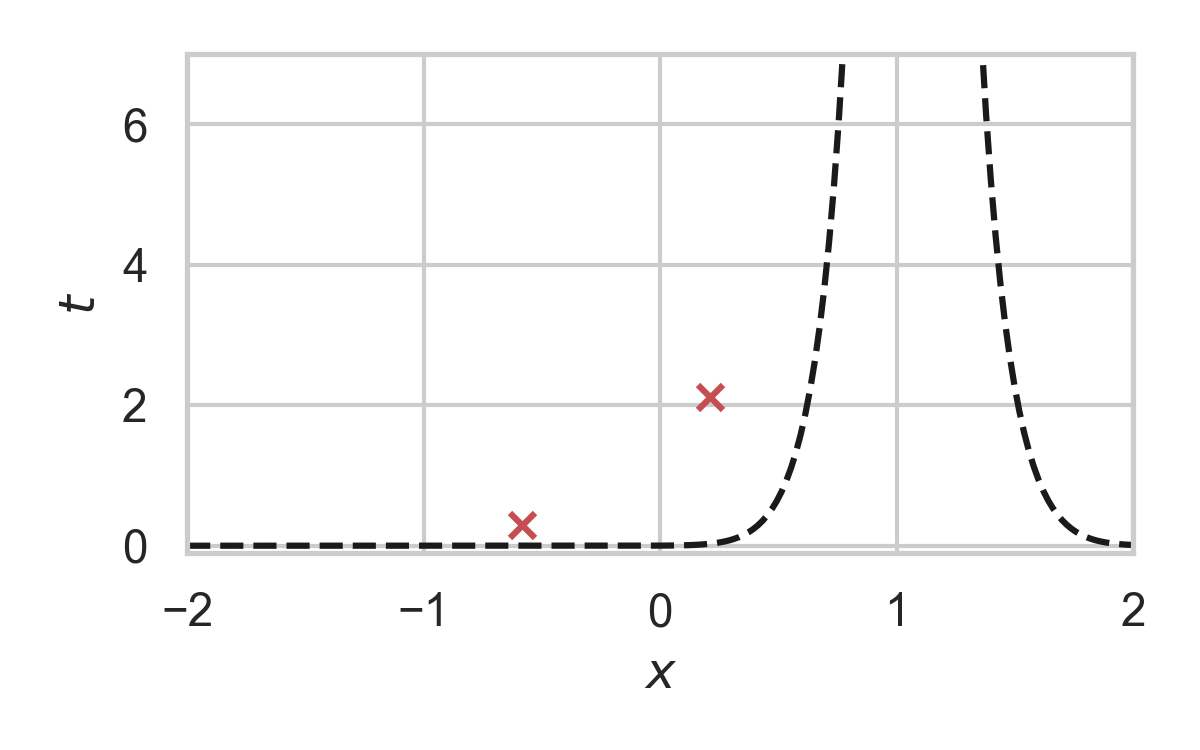
gprs_2.png

8.16. GPRS with \(P = \mathcal{N}(0, 1), Q = \mathcal{N}(1, 1/16)\)

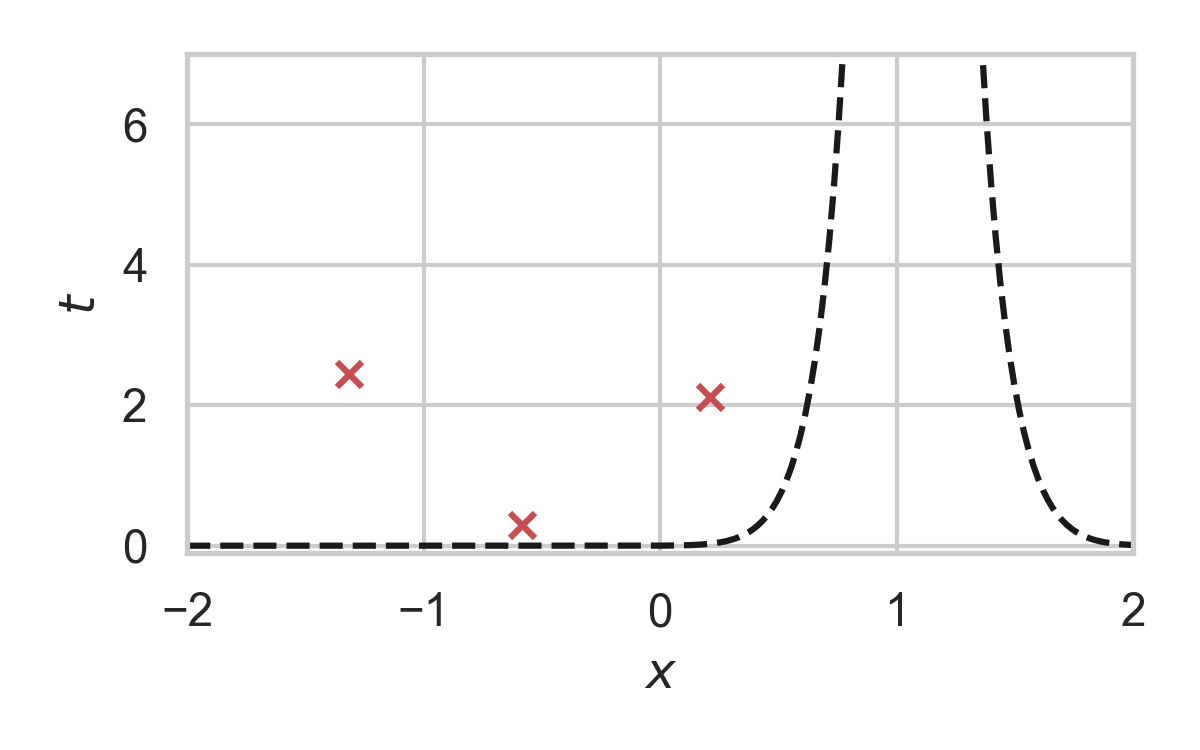
gprs_3.png

8.17. GPRS with \(P = \mathcal{N}(0, 1), Q = \mathcal{N}(1, 1/16)\)

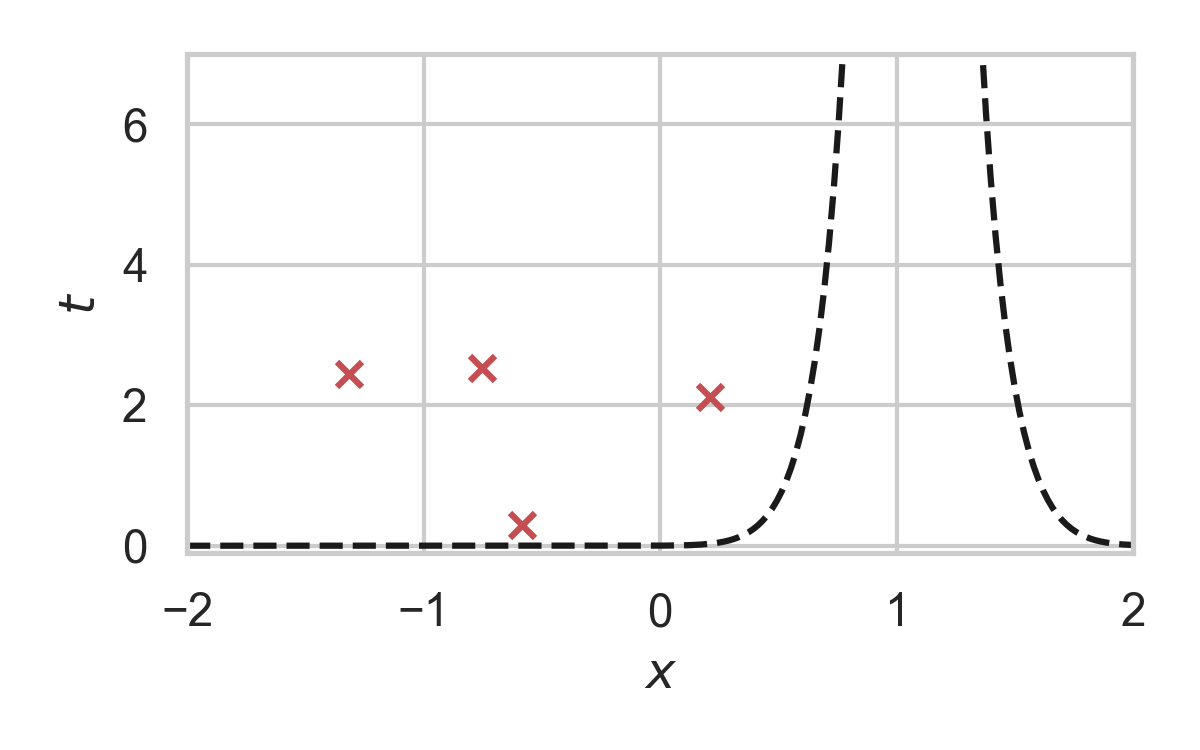
gprs_4.png

8.18. GPRS with \(P = \mathcal{N}(0, 1), Q = \mathcal{N}(1, 1/16)\)

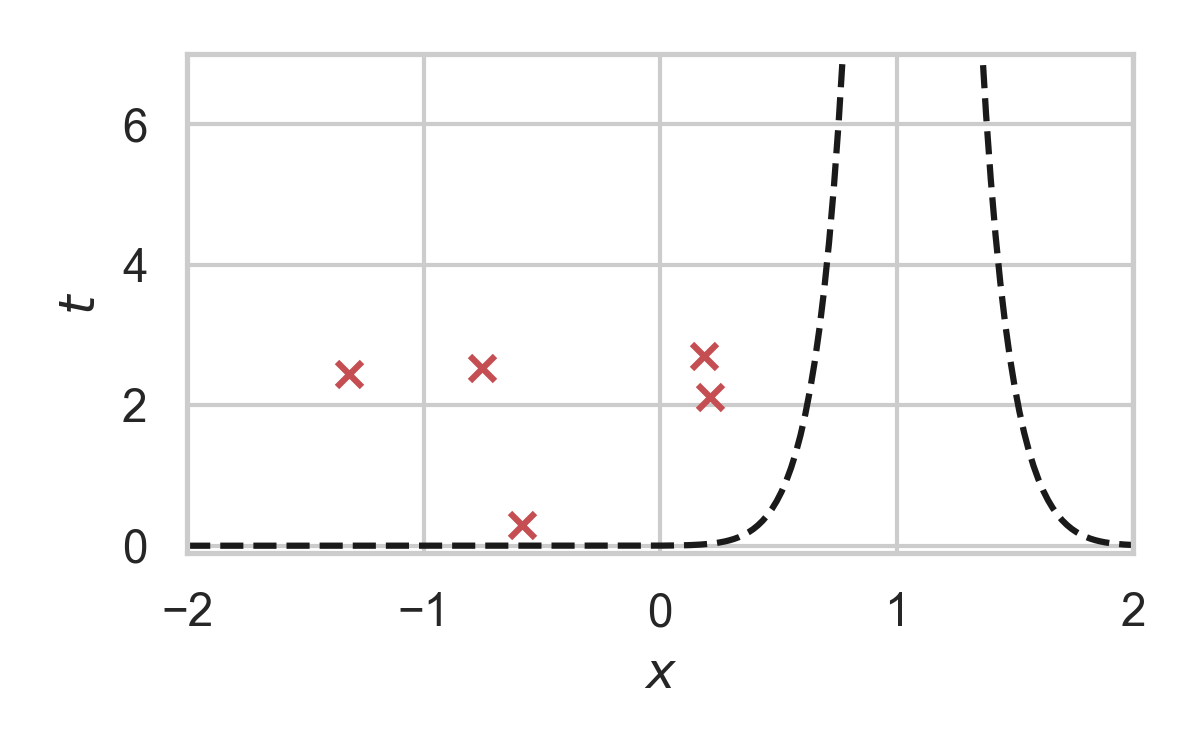
gprs_5.png

8.19. GPRS with \(P = \mathcal{N}(0, 1), Q = \mathcal{N}(1, 1/16)\)

gprs_accept.png

8.20. How to find the graph?

\[ \varphi(x) = \int_0^{\frac{dQ}{dP}(x)} \frac{1}{w_Q(\eta) - \eta \cdot w_P(\eta)} \, d\eta, \]

where \[ w_P(h) = \mathbb{P}_{Z \sim P}\left[\frac{dQ}{dP}(Z) \geq h \right] \] \[ w_Q(h) = \mathbb{P}_{Z \sim Q}\left[\frac{dQ}{dP}(Z) \geq h \right] \]

8.21. Analysis of GPRS

Codelength

\begin{align} \mathbb{H}[X \mid S] &\leq I[X; Y] + \log (I[X; Y] + 1) \\ &\quad + 2 + \frac{1}{1 + I[X; Y] \cdot \ln 2} \end{align}

Runtime

\[ \mathbb{E}[K \mid Y] = \exp(D_{\infty}[P_{X \mid Y} \Vert P_X]) \]

8.22. Speeding up GPRS

gprs_accept.png

8.23. Fast GPRS with \(P = \mathcal{N}(0, 1), Q = \mathcal{N}(1, 1/16)\)

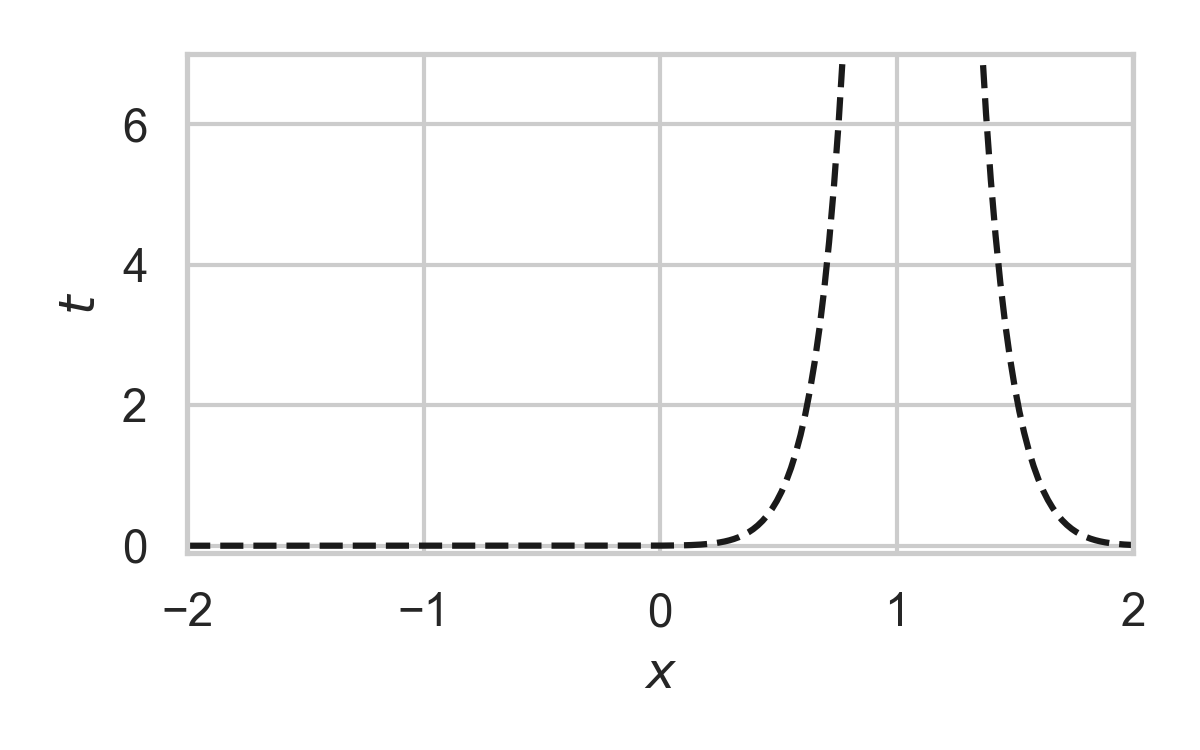
fast_gprs_0.png

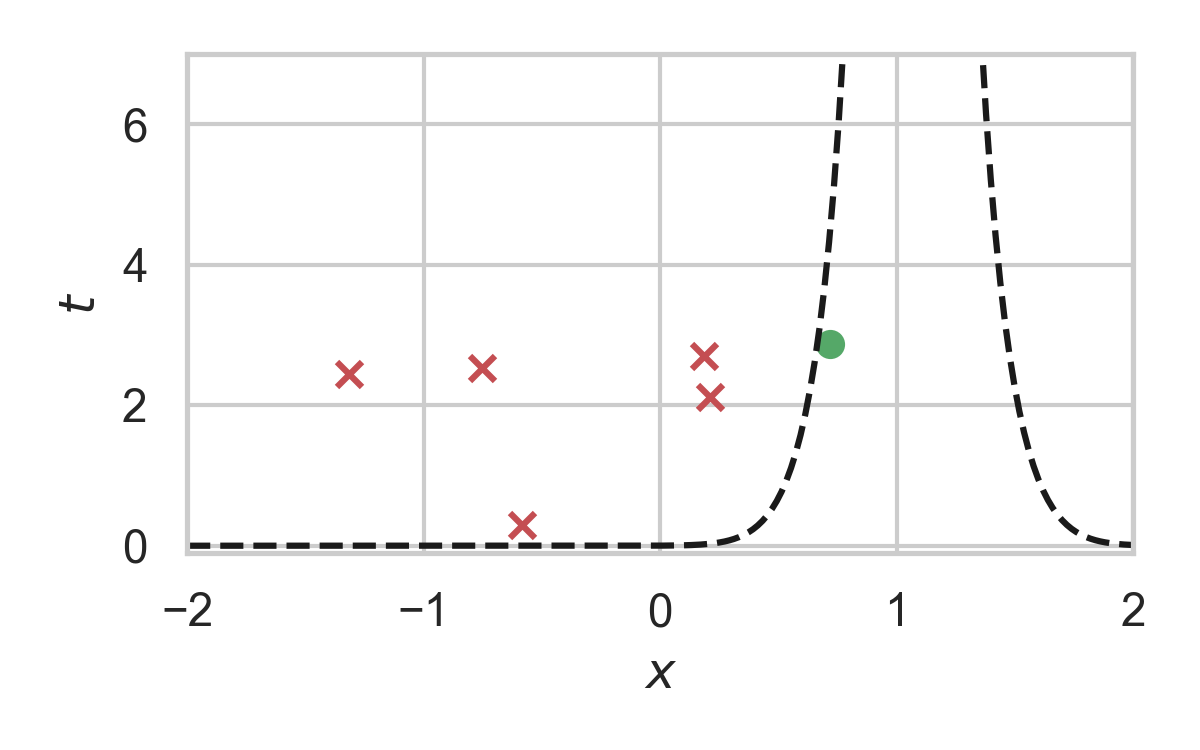
8.24. Fast GPRS with \(P = \mathcal{N}(0, 1), Q = \mathcal{N}(1, 1/16)\)

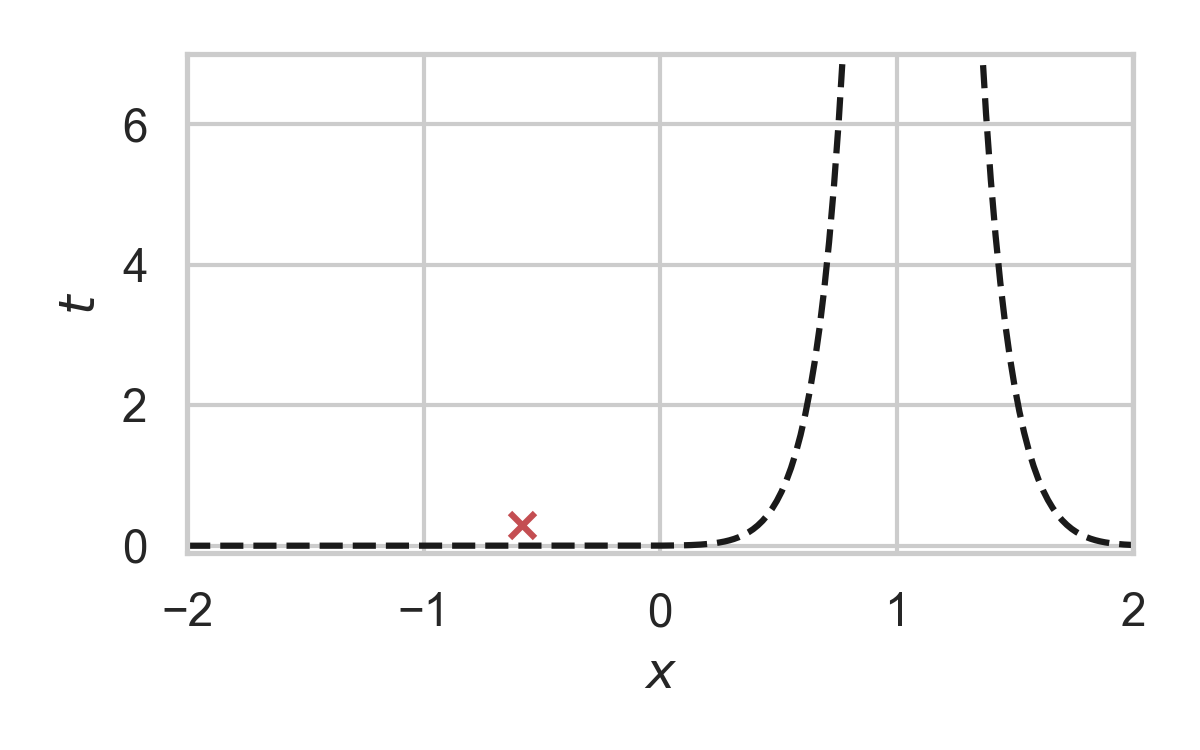
fast_gprs_1.png

8.25. Fast GPRS with \(P = \mathcal{N}(0, 1), Q = \mathcal{N}(1, 1/16)\)

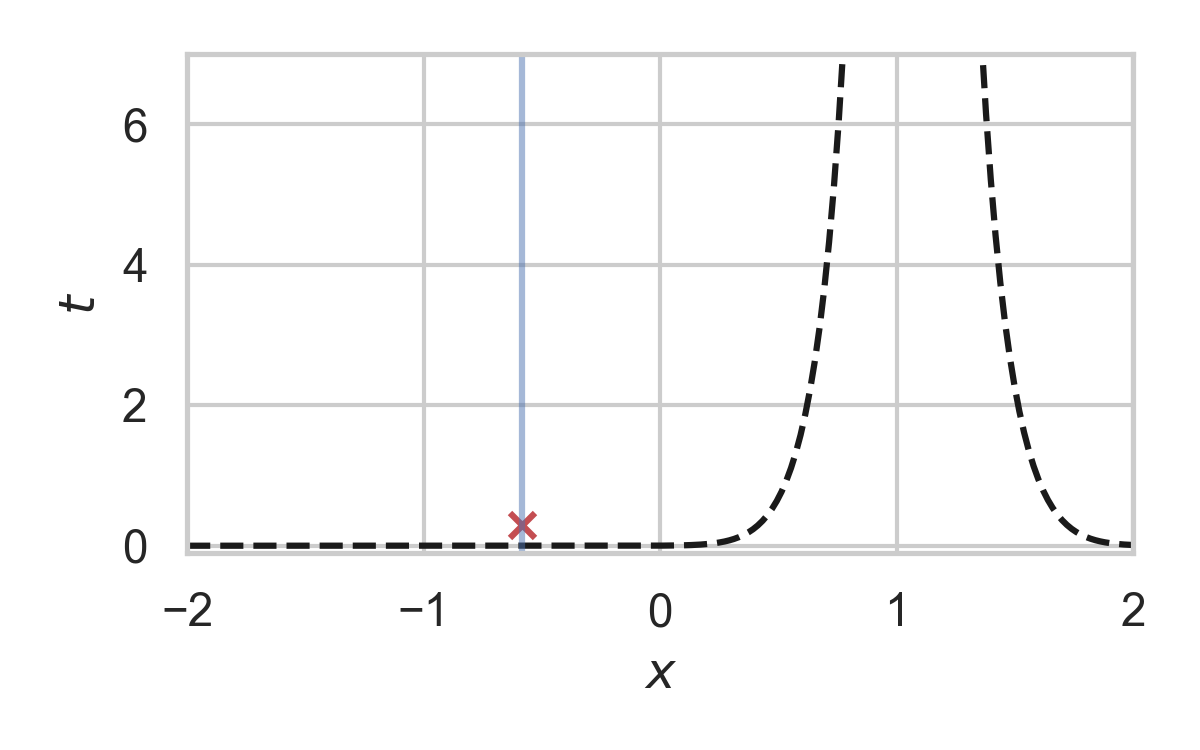
fast_gprs_2.png

8.26. Fast GPRS with \(P = \mathcal{N}(0, 1), Q = \mathcal{N}(1, 1/16)\)

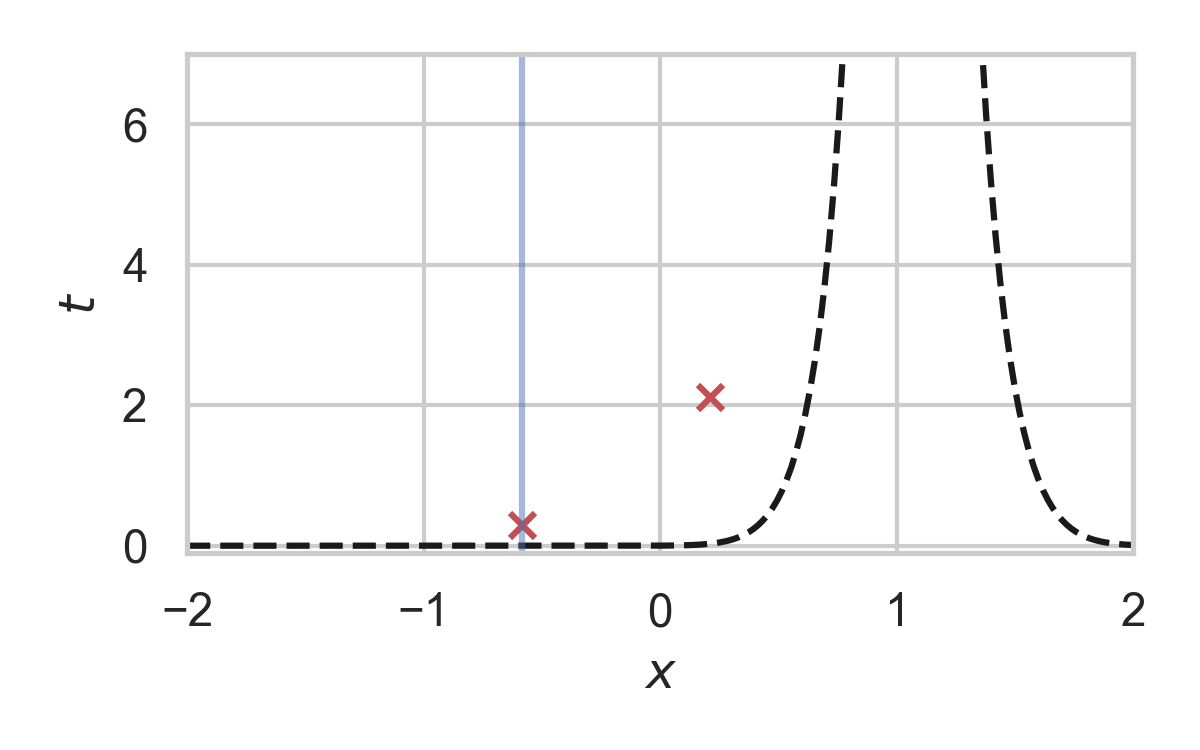
fast_gprs_3.png

8.27. Fast GPRS with \(P = \mathcal{N}(0, 1), Q = \mathcal{N}(1, 1/16)\)

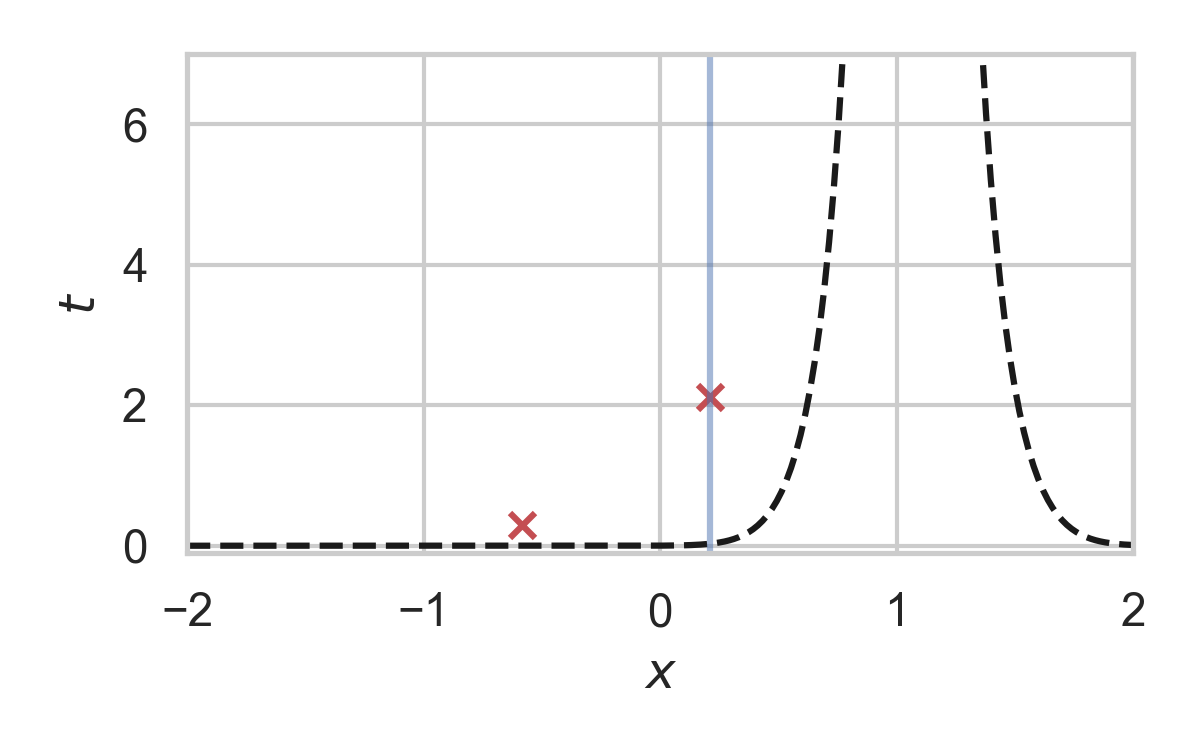
fast_gprs_4.png

8.28. Fast GPRS with \(P = \mathcal{N}(0, 1), Q = \mathcal{N}(1, 1/16)\)

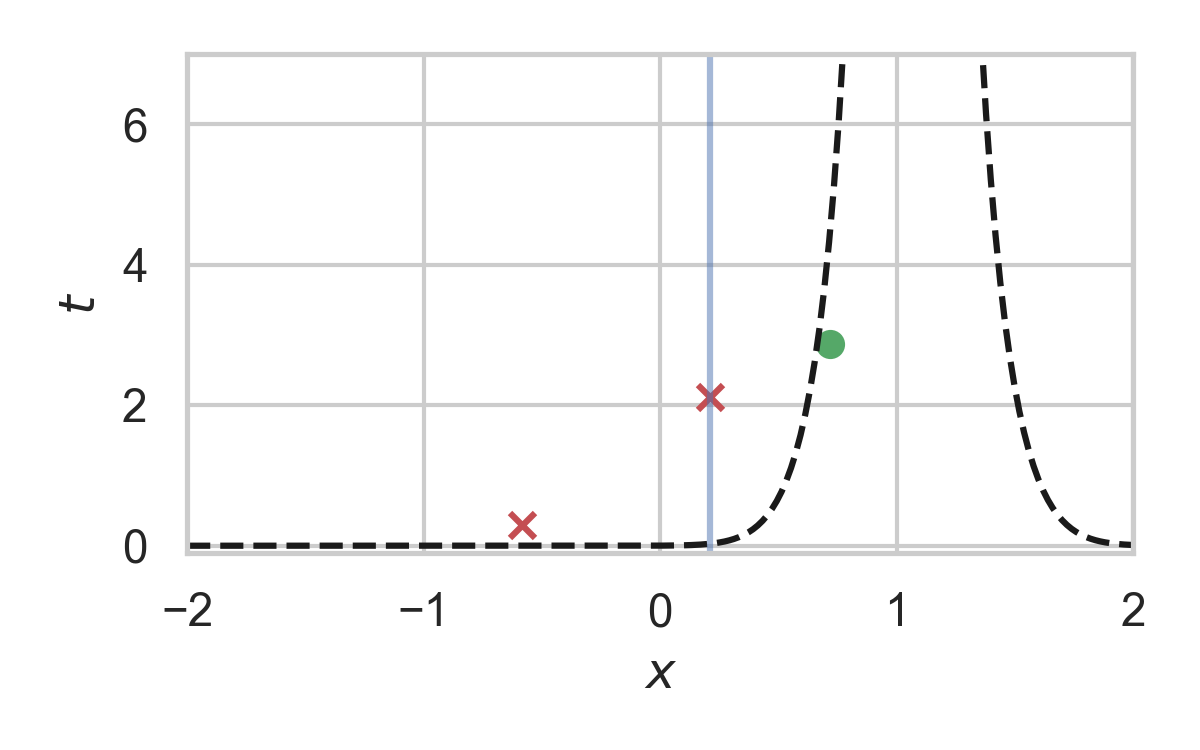
fast_gprs_5.png

8.29. Analysis of faster GPRS

Now, encode search path \(\pi\).

\(\mathbb{H}[\pi] \leq I[X; Y] + \log(I[X; Y] + 1) + \mathcal{O}(1)\)

\(\mathbb{E}[\lvert\pi\rvert] = \mathcal{O}(I[X; Y])\)

This is optimal.

9. Take home message: GPRS

  • GPRS is a rejection sampler using Poisson processes
  • Can be used for relative entropy coding
  • Has an optimally efficient variant for 1D, unimodal distributions

10. Some recent results

šŸ¤” REC: A misnomer?

10.1. Coding Efficiency Revisited

REC coding efficiency: \[ {\color{red} I[X; Y]} \leq \mathbb{H}[X \mid S] \leq {\color{red} I[X; Y]} + {\color{blue} \log (I[X; Y] + 1) + 4} \]

Doesn't collapse onto Shannon's source coding theorem.

10.2. Rewriting the KL Divergence

\begin{align} D_{KL}[Q || P] &= \int_\Omega \frac{dQ}{dP}(x) \cdot \log \frac{dQ}{dP}(x) \, dP(x) \\ &= \log e + \int_0^\infty \underbrace{\mathbb{P}_{Z \sim P}\left[ \frac{dQ}{dP}(Z) \geq h \right]}_{= w_P(h)} \cdot \log h \, dh \end{align}

10.3. A New Measure of Efficiency

\[ D_{KL}[Q || P] = \log e - \int_0^\infty w_P(h) \log \frac{1}{h} \, dh \]

\[ D_{CS}[Q || P] = -\int_0^\infty w_P(h) \log w_P(h) \, dh \]

10.4. Properties of \(D_{CS}\)

  1. \(D_{CS}[Q || P] \geq 0\), equality when \(Q = P\).
  2. \(D_{CS}[\delta_x || P] = -\log P(x)\).

  3. In the rejection sampling setup (Goc & F.):

    \begin{align} D_{KL}[Q || P] &\leq D_{CS}[Q || P] \\ &\ {\color{red} \leq}\ \mathbb{H}[X \mid S, Y = y] \\ &\ {\color{blue} \leq}\ D_{CS}[Q || P] + \log(1 + e) \\ &\leq D_{KL}[Q || P] + \log(D_{KL}[Q || P] + 1) \\ & \quad\quad + \log(1 + e) + o(1) \end{align}

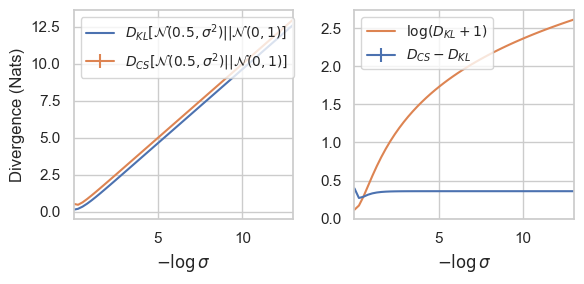
10.5. Some Empirical Results I

\begin{align} D_{KL}[\mathcal{L}(0, b) || \mathcal{L}(0, 1)] &= b - \ln b - 1 \\ D_{CS}[\mathcal{L}(0, b) || \mathcal{L}(0, 1)] &= b - \psi\left(\frac{1}{b}\right) + \gamma - 1 \end{align}

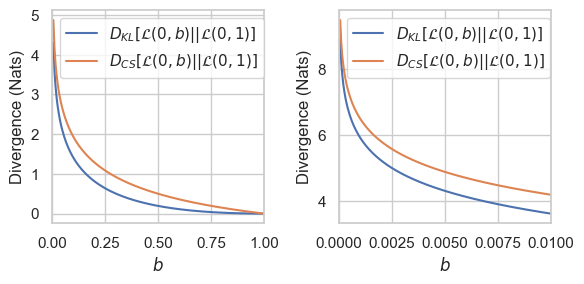
laplace_divergences.png

10.6. Some Empirical Results II

gauss_1d_divergences.png

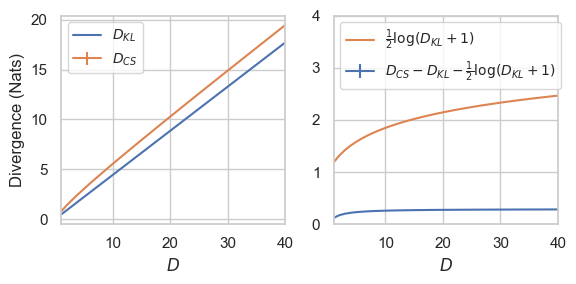
10.7. Some Empirical Results III

gauss_nd_divergences.png

11. References

11.1. References I

  • E. Agustsson and L. Theis. "Universally quantized neural compression" In NeurIPS 2020.
  • C. Blundell, J. Cornebise, K. Kavukcuoglu and D. Wierstra. Weight uncertainty in neural network. In ICML 2015.
  • E. Dupont, A. Golinski, M. Alizadeh, Y. W. Teh and Arnaud Doucet. "COIN: compression with implicit neural representations" arXiv preprint arXiv:2103.03123, 2021.

11.2. References II

  • G. F. ā€œGreedy Poisson Rejection Samplingā€ NeurIPS 2023, to appear.
  • G. F.*, S. Markou*, and J. M. Hernandez-Lobato. "Fast relative entropy coding with A* coding". In ICML 2022.
  • D. Goc and G. F. ā€œOn Channel Simulation Conjecturesā€ unpublished.

11.3. References III

  • Z. Guo*, G. F.*, J. He, Z. Chen and J. M. Hernandez Lobato, ā€œCompression with Bayesian Implicit Neural Representationsā€ NeurIPS 2023, to appear.
  • P. Harsha, R. Jain, D. McAllester, and J. Radhakrishnan, ā€œThe communication complexity of correlation,ā€ IEEE Transactions on Information Theory, vol. 56, no. 1, pp. 438ā€“449, 2010.
  • M. Havasi, R. Peharz, and J. M. HernaĢndez-Lobato. "Minimal Random Code Learning: Getting Bits Back from Compressed Model Parameters" In ICLR 2019.

11.4. References IV

  • J. He*, G. F.*, Z. Guo and J. M. Hernandez Lobato, ā€œRECOMBINER: Robust and Enhanced Compression with Bayesian Implicit Neural Representationsā€ unpublished.
  • C. T. Li and A. El Gamal, ā€œStrong functional representation lemma and applications to coding theorems,ā€ IEEE Transactions on Information Theory, vol. 64, no. 11, pp. 6967ā€“6978, 2018.

11.5. References V

  • L. Theis and E. Agustsson. On the advantages of stochastic encoders. arXiv preprint arXiv:2102.09270.
  • L. Theis, T. Salimans, M. D. Hoffman and F. Mentzer (2022). Lossy compression with Gaussian diffusion. arXiv preprint arXiv:2206.08889.

12. Other material

lossless_rec.png