Adaptive Greedy Rejection Sampling

Gergely Flamich and Lucas Theis

26/06/2023

gergely-flamich.github.io

1. In Collaboration With

Lucas Theis

2. Background

2.1. Channel Simulation

Correlated r.v.s \(X, Y \sim P_{X, Y}\)

Alice receives \(Y \sim P_Y\)

Bob wants to simulate \(X \sim P_{X \mid Y}\)

How many bits does Alice need to send to Bob?

When common randomness \(S\) available (SFRL): \[ H[X \mid S] \leq I[X; Y] + \log (I[X; Y] + 1) + 4. \]

2.2. Lossy compression

3. Greedy Rejection Sampling

3.1. Greedy Rejection Sampling

Originally proposed by Harsha et al. (2006) for discrete distributions.

We extend it to Borel probability measures over Polish spaces.

3.2. GRS Example

Target \(Q = \mathcal{N}(\mu, \sigma^2)\), proposal \(P = \mathcal{N}(0, 1)\)

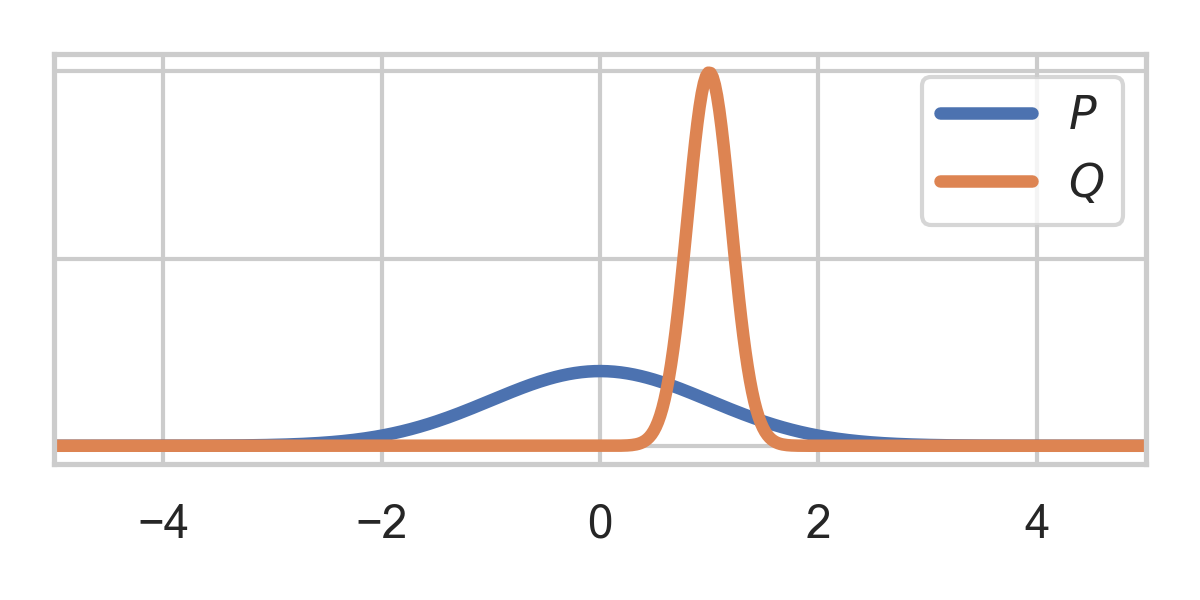
Change of variables: \(U = F_P(X)\)

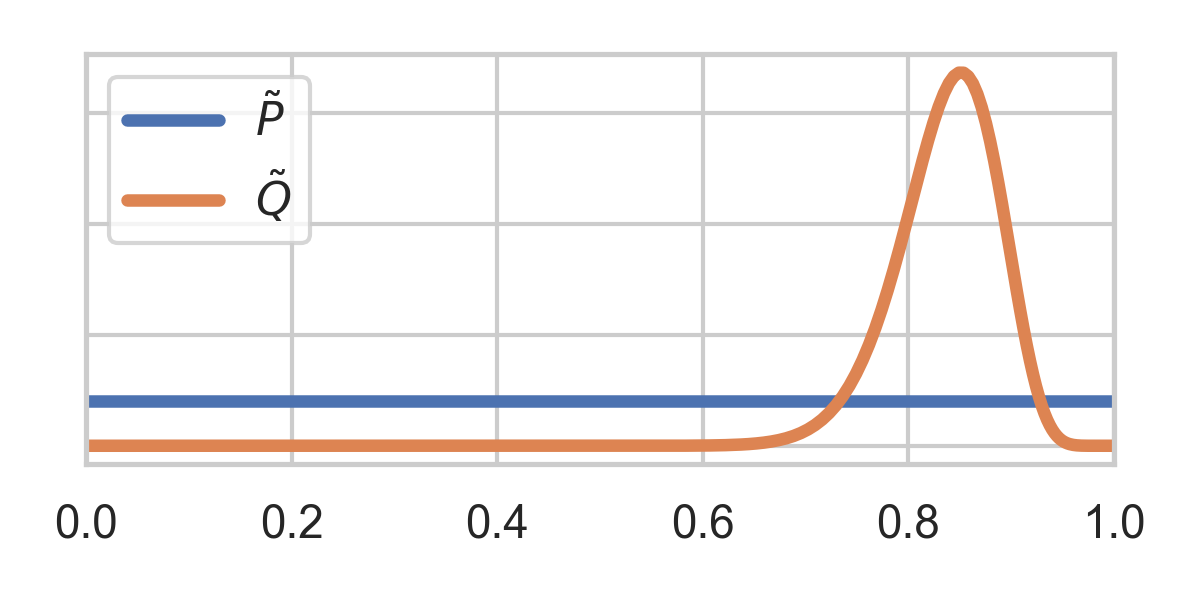
3.3. GRS Example Cont'd

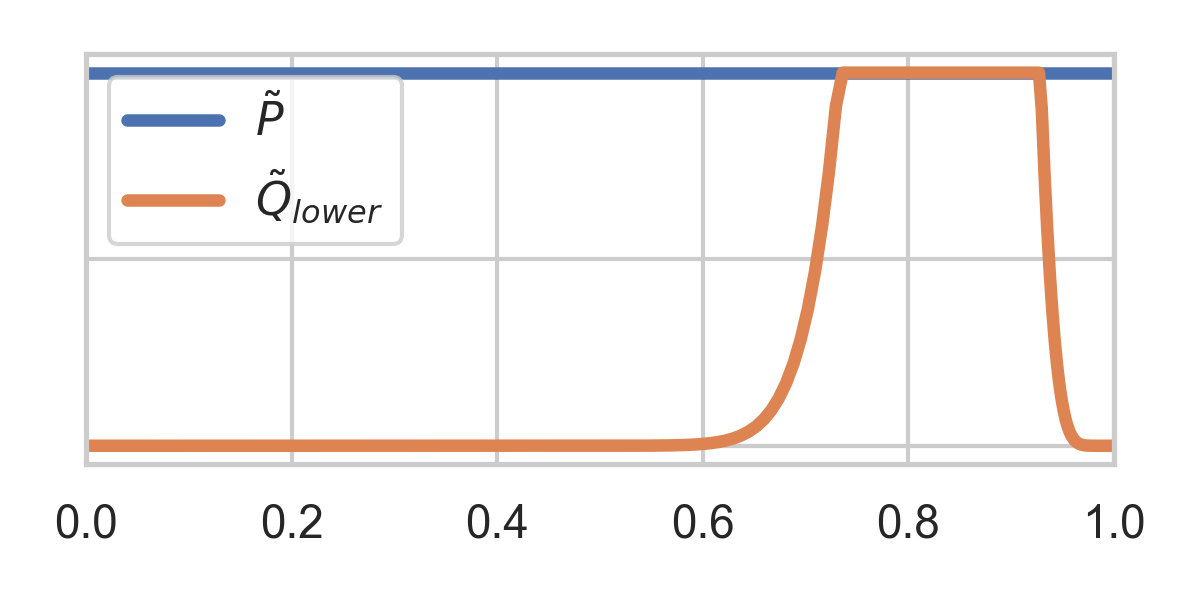
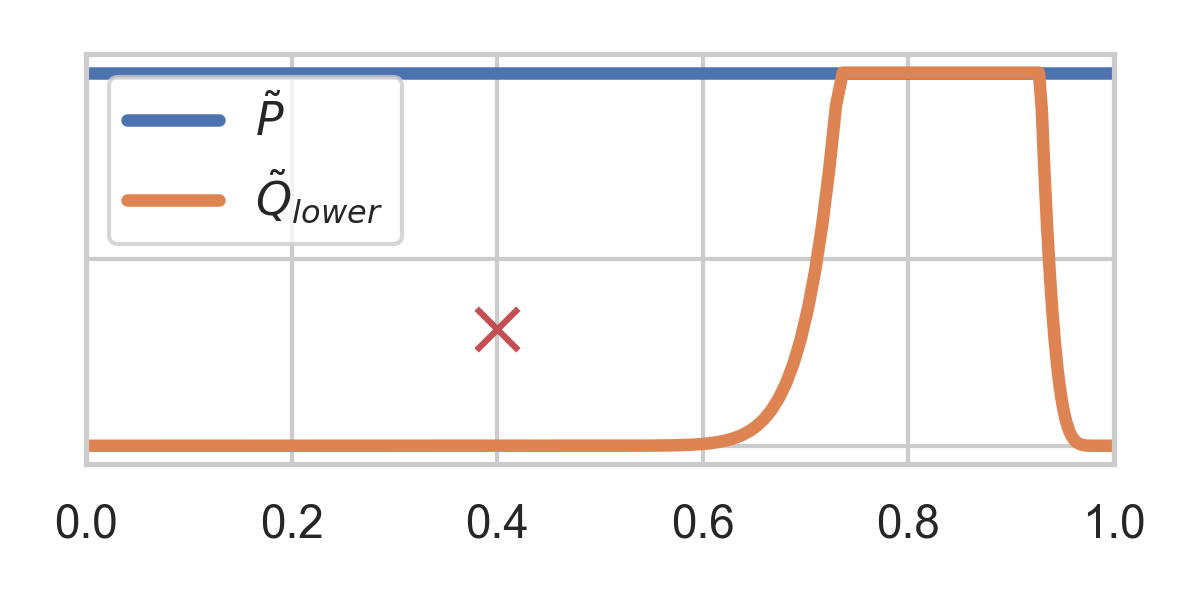
If rejected, normalize upper half and repeat:

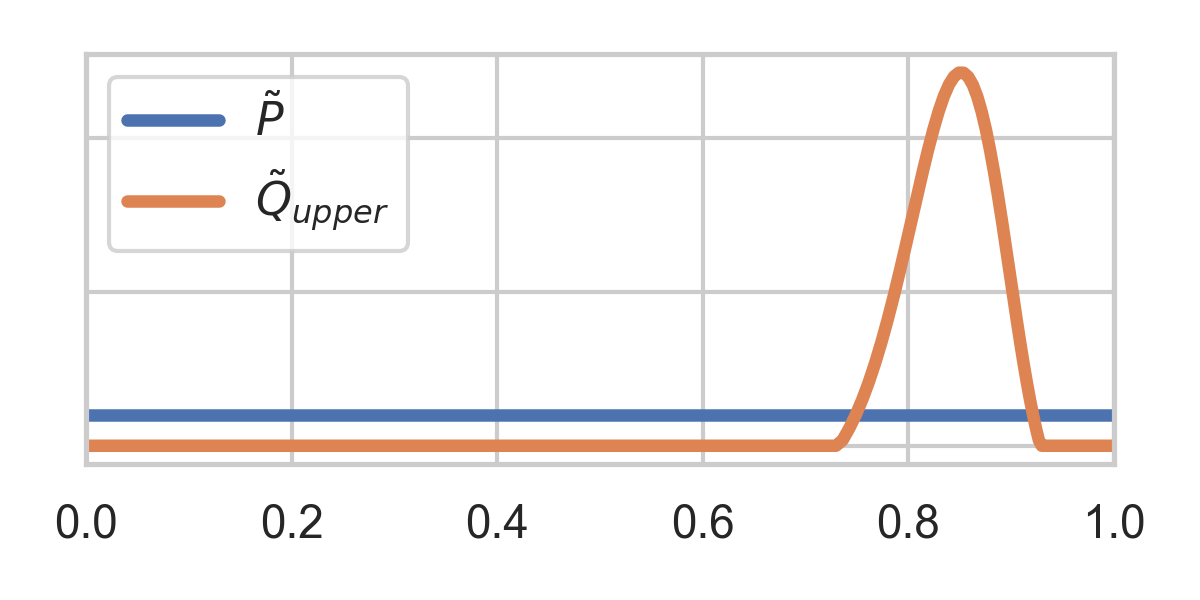
3.4. GRS Coding

To encode sample:

Simulate \(X_i \sim P\) with common randomness \(S\)

Count number of rejections \(K\)

Transmit \(K\) using a Zeta coding distribution: \[ \zeta(k \mid \alpha) \propto k^{-\alpha} \]

3.5. GRS Analysis

For fixed \(Q\) and \(P\): \[ H[K] \leq D_{KL}[Q \,\Vert\, P] + \log(D_{KL}[Q \,\Vert\, P] + 1) + 4 \]

When \(Q \gets P_{X \mid Y}\) and \(P \gets P_X\), average over \(Y\): \[ H[K] \leq I[X; Y] + \log(I[X; Y] + 1) + 4 \]

3.6. GRS Analysis Cont'd

\[ \mathbb{E}[K + 1] = 2^{D_{\infty}[Q \,\Vert\, P]} \] where \[ D_{\infty}[Q \,\Vert\, P] = \log\left(\mathrm{ess\,sup}_{x \in \Omega}\left\{\frac{dQ}{dP}(x)\right\}\right) \]

3.7. The Gaussian Case

\[ X \mid \mu \sim \mathcal{N}(\mu, \rho^2I), \quad \mu \sim \mathcal{N}(0, \sigma^2I) \]

Then: \[ P_{X} = \mathcal{N}(0, (\sigma^2 + \rho^2)I) \]

Now, we find: \[ \mathbb{E}[K + 1] = \infty \]

3.8. The Gaussian Case: Overdispersion

Use overdispersed marginal: \[ P_s = \mathcal{N}(0, (s^2 + \rho^2)I), \quad \sigma^2 < s^2 \]

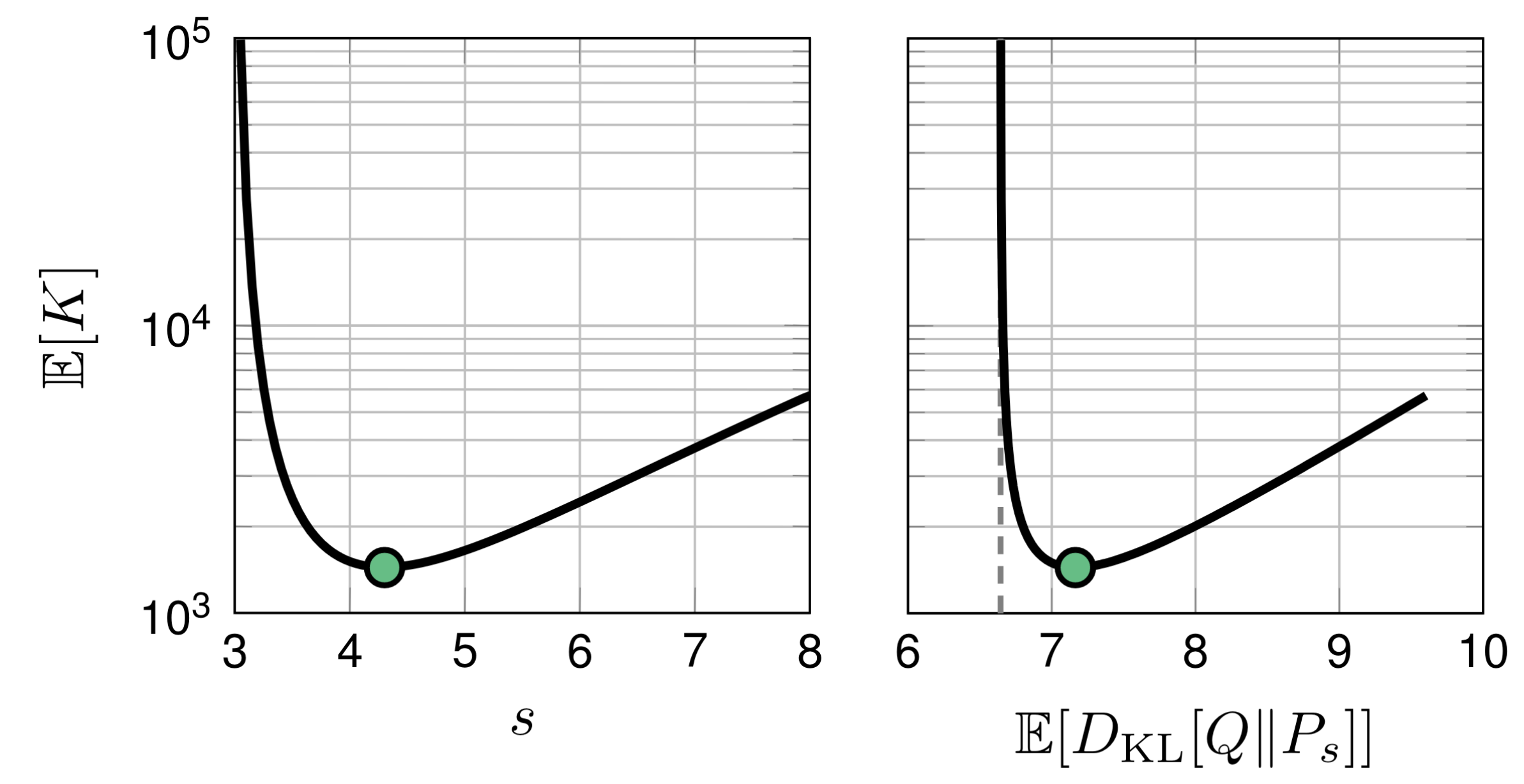
4. Adaptive Greedy Rejection Sampling

4.1. GRS Example Revisited

Most of sample space useless, adapt proposal:

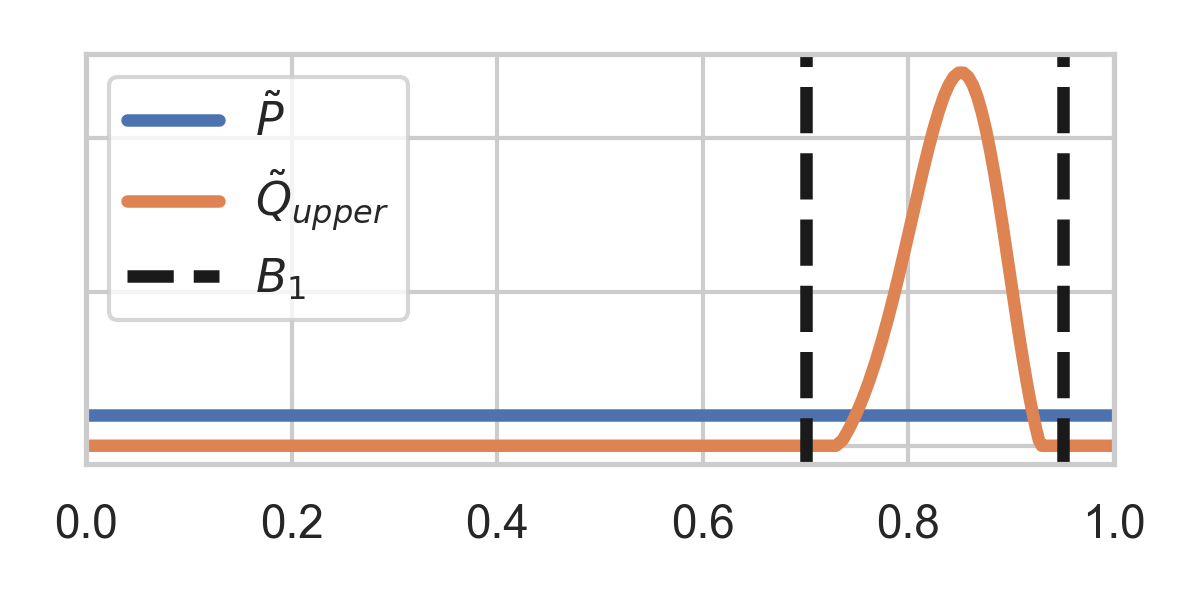
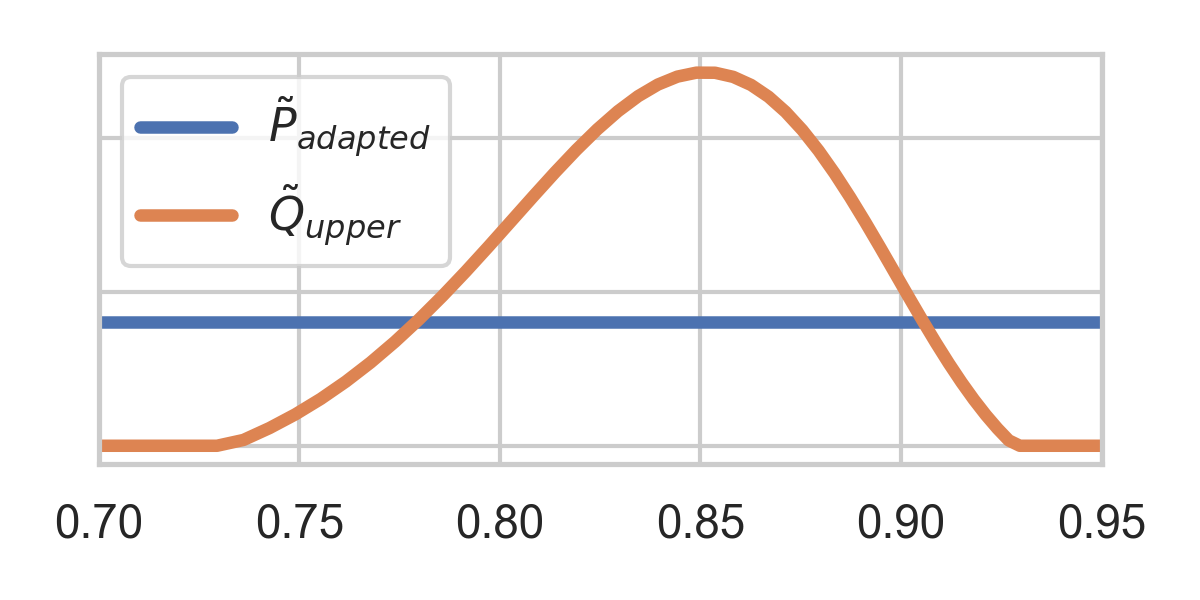
4.2. AGRS Coding

Need suitable sequence of bounds \(B_1, B_2, \dots\).

Need to communicate \(K, B_K\)!

Theorem: \[ H[K] \leq C + \log(C + 1) + 3.63, \] where \(C = I[X;Y] + \mathbb{E}[\log P(B_{m_{K}})]\).

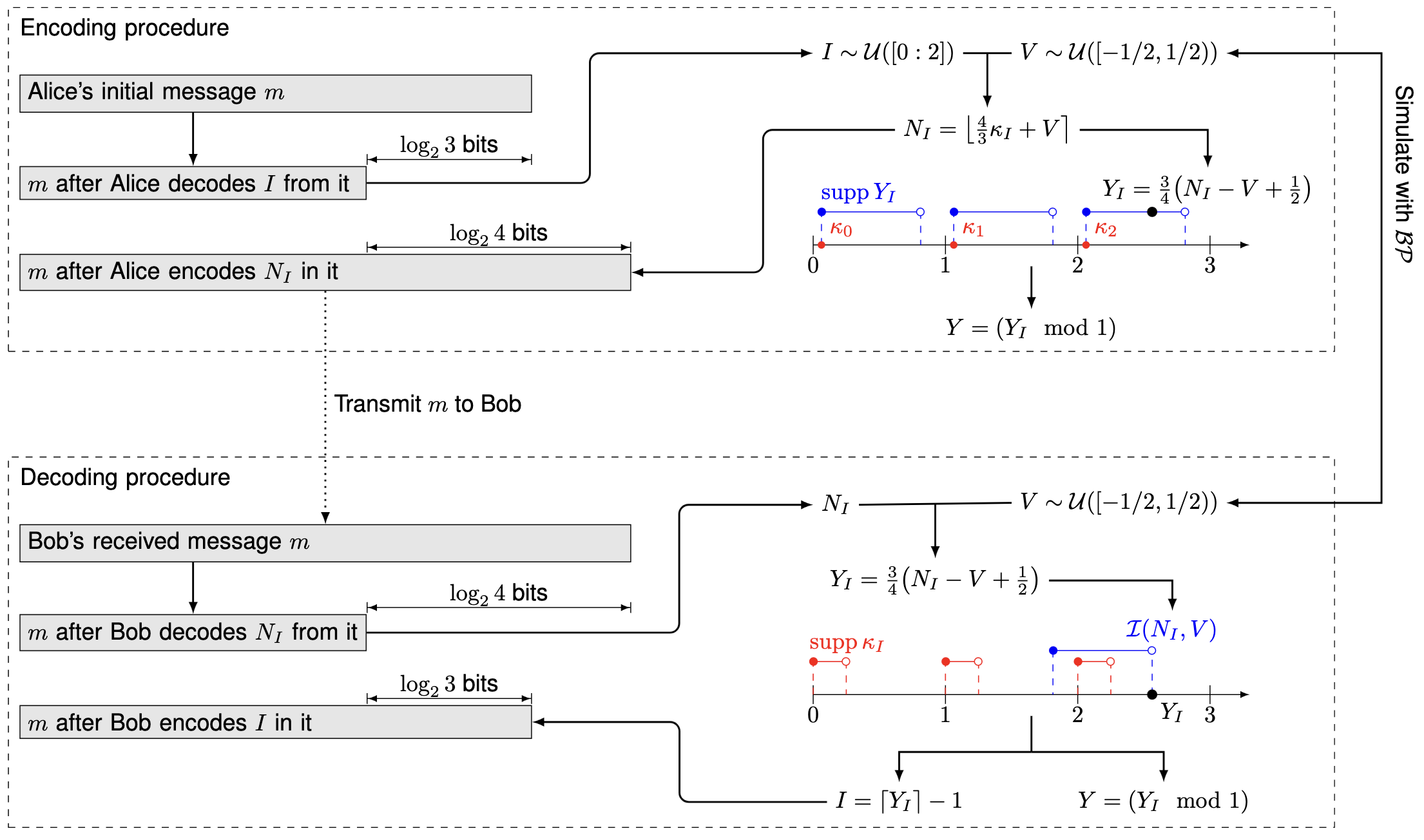
4.3. AGRS with Dithered Quantization

\[ \lfloor c + U \rceil - U \stackrel{d}{=} c + U' \] where \(U, U' \sim \mathrm{Unif}(-1/2, 1/2)\)

If \(c \in [1/2, M - 3/2)\), then \(\lfloor c + U \rceil \in [0:M - 1]\).

\[ \frac{\lfloor c + U \rceil - U}{M} \sim \mathrm{Unif}\left(\frac{c}{M} - \frac{1}{2M}, \frac{c}{M} + \frac{1}{2M} \right). \]

4.4. AGRS with Dithered Quantization Cont'd

With DQ, we can encode any bound with size \(1 / M\).

What about bounds with arbitrary rational sizes?

DQ + Bits-back: Bits-back Quantization (BBQ)

4.5. AGRS for 1D Gaussians

Apply AGRS to our Gaussian example:

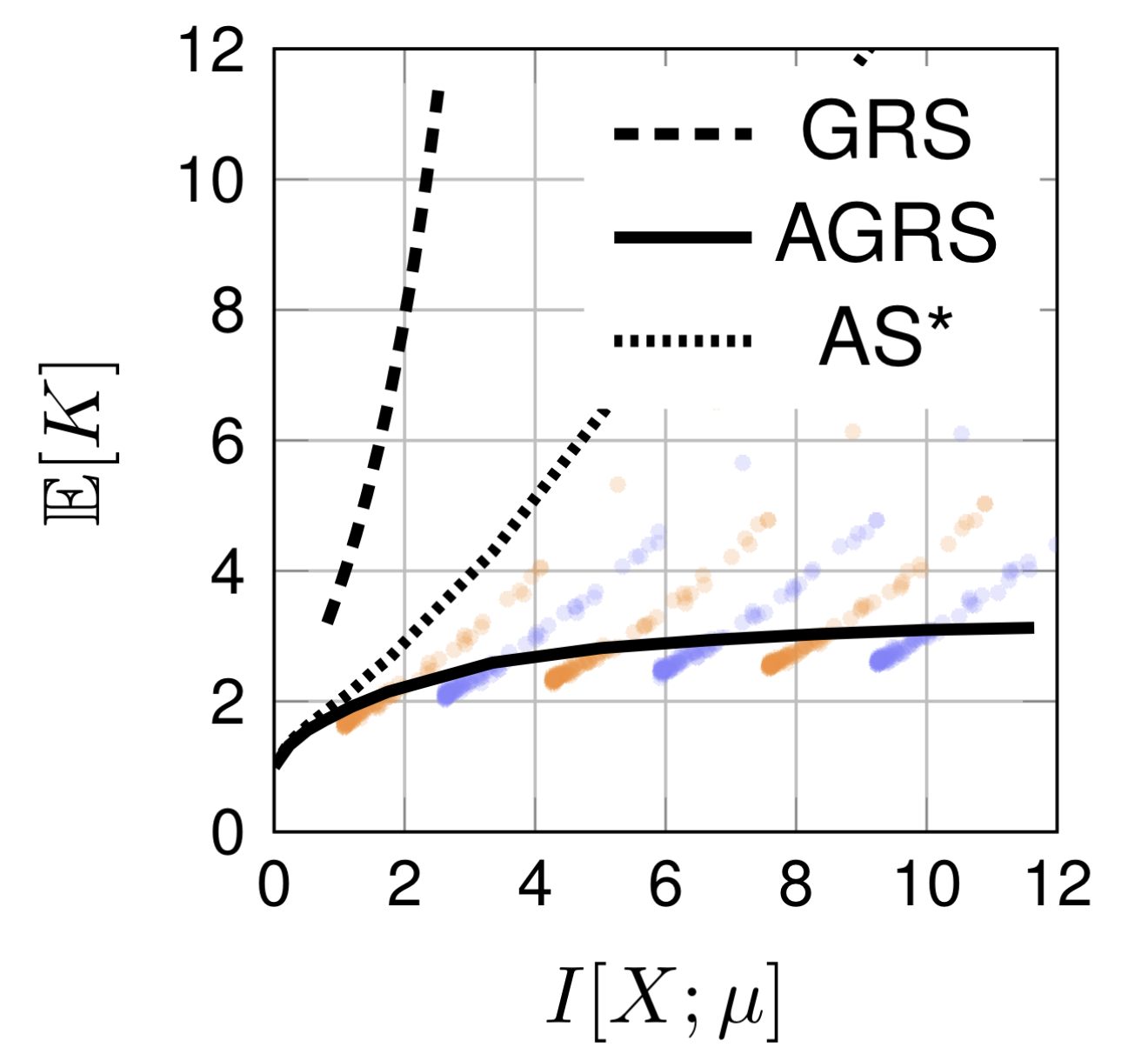
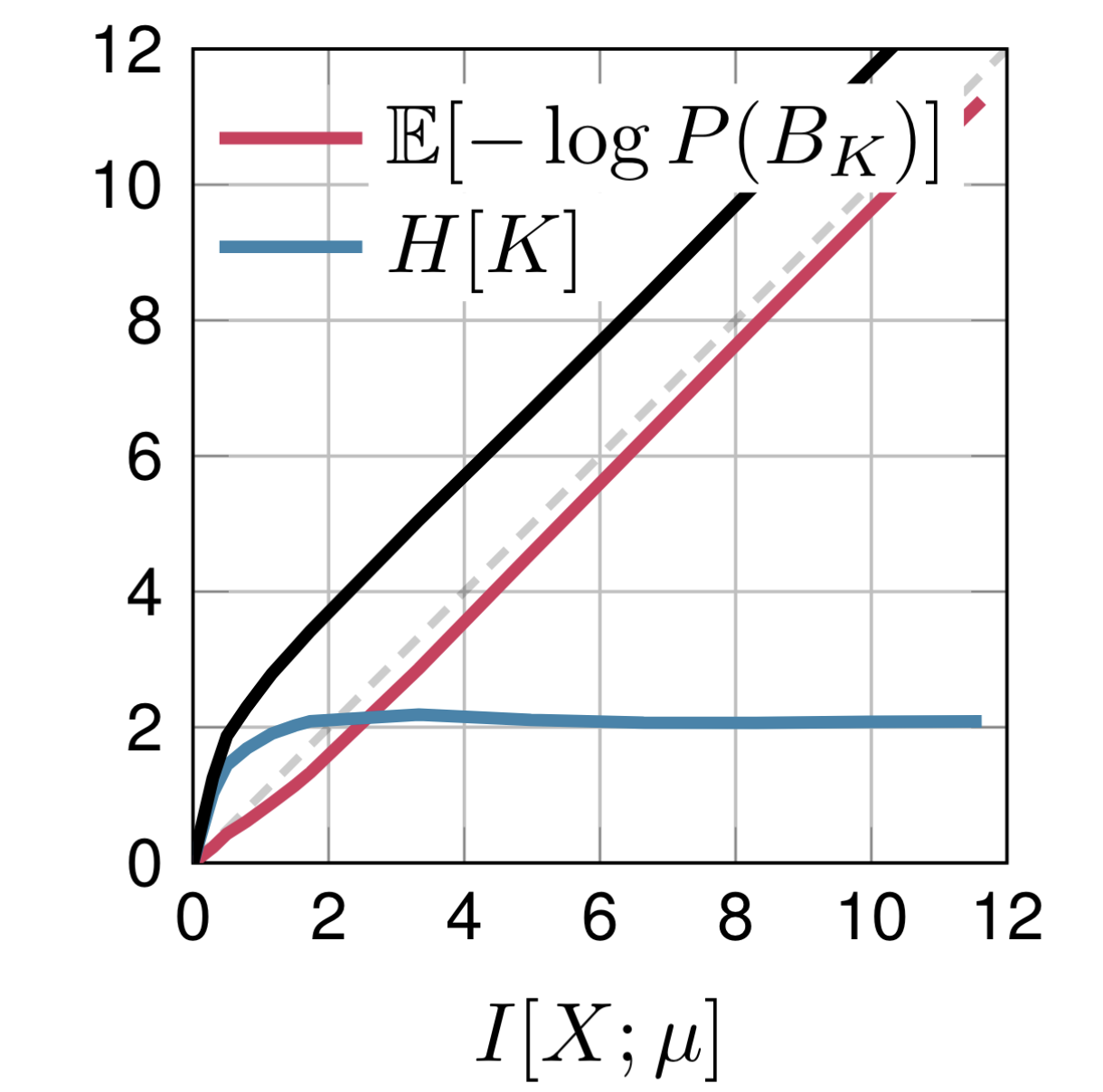
5. Future directions

Is there a sampling algorithm with \(\mathcal{O}\left(2^{D_{KL}[Q \,\Vert\, P]}\right)\) or is \(2^{D_{\infty}[Q \,\Vert\, P]}\) tight?
Connection to Poisson Functional Representation (Li and El Gamal, 2017)? See Greedy Poisson Rejection Sampling (F., 2023)
Specialized algorithms for Gaussians?

6. References

P. Harsha, R. Jain, D. McAllester, and J. Radhakrishnan, “The communication complexity of correlation,” IEEE Transactions on Information Theory, vol. 56, no. 1, pp. 438–449, 2010.
C. T. Li and A. El Gamal, “Strong functional representation lemma and applications to coding theorems,” IEEE Transactions on Information Theory, vol. 64, no. 11, pp. 6967–6978, 2018.
F. “Greedy Poisson Rejection Sampling,” arXiv preprint arXiv:2305.15313, 2023.