1. Notation

• \(\lVert x \rVert_p \stackrel{def}{=} \left( \sum_{k = 1}^n \lvert x_k \rvert^p \right)^{1 / p}\)
• \(B_p^n \stackrel{def}{=} \left\{x \in \mathbb{R}^n \mid \lVert x \rVert_p \leq 1 \right\}\)
• \(S_p^n \stackrel{def}{=} \partial B^{n + 1}_p\)
• \(\mathcal{B}_p^n\) - uniform distribution on \(B_p^n\)
• \(\mathcal{S}_p^n\) - uniform distribution on \(S_p^n\).

2. In Pictures

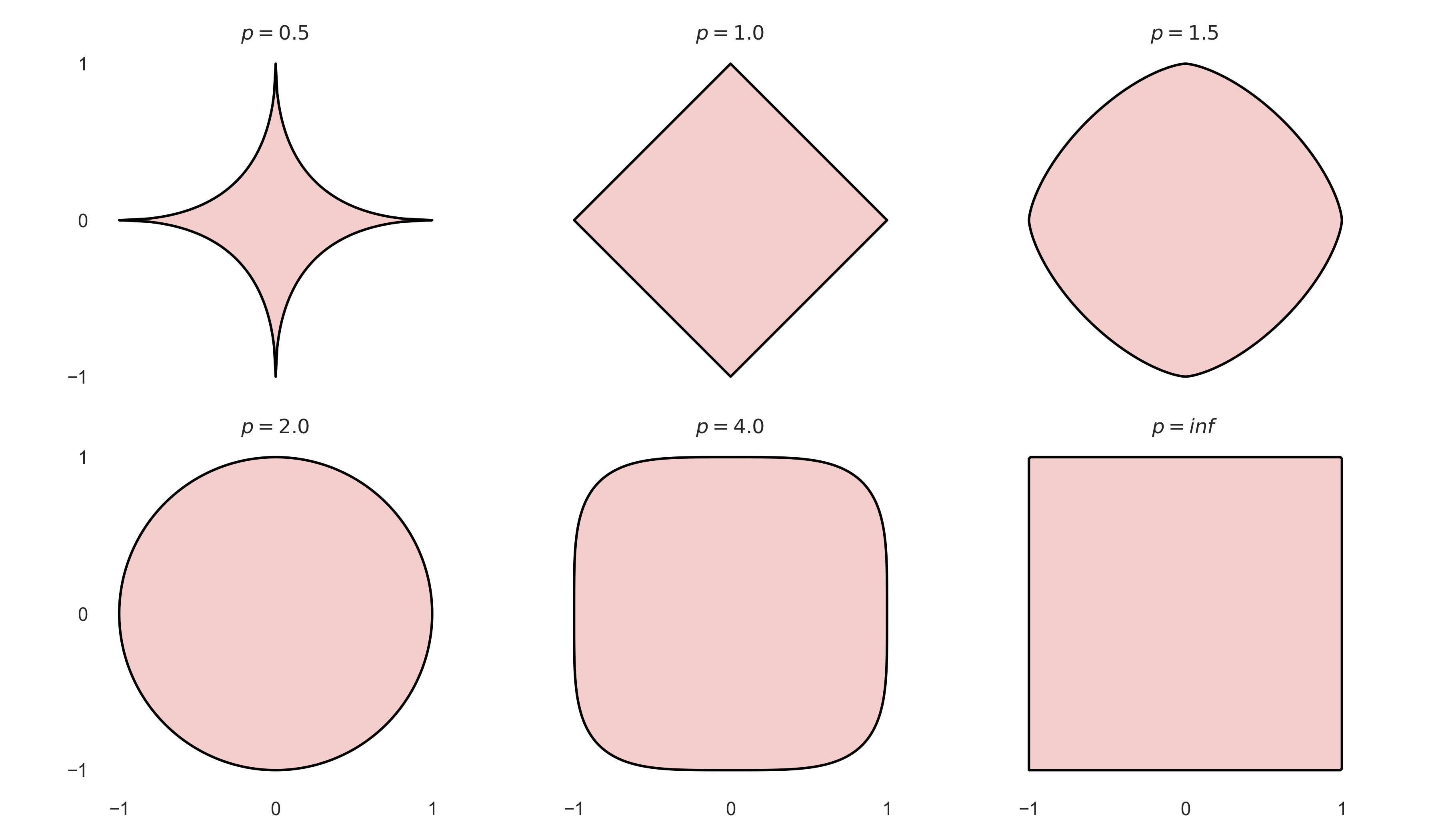
3. First attempt

• For \(\mathcal{B}_p^n:\) Rejection sample
• Uniform proposal on \(C^n = [-1, 1]^n\)

4. Problem w/ first attempt

\(\text{Accept prob} = \mathrm{Vol}(B_p^n) \, / \, \mathrm{Vol}(C^n)\)

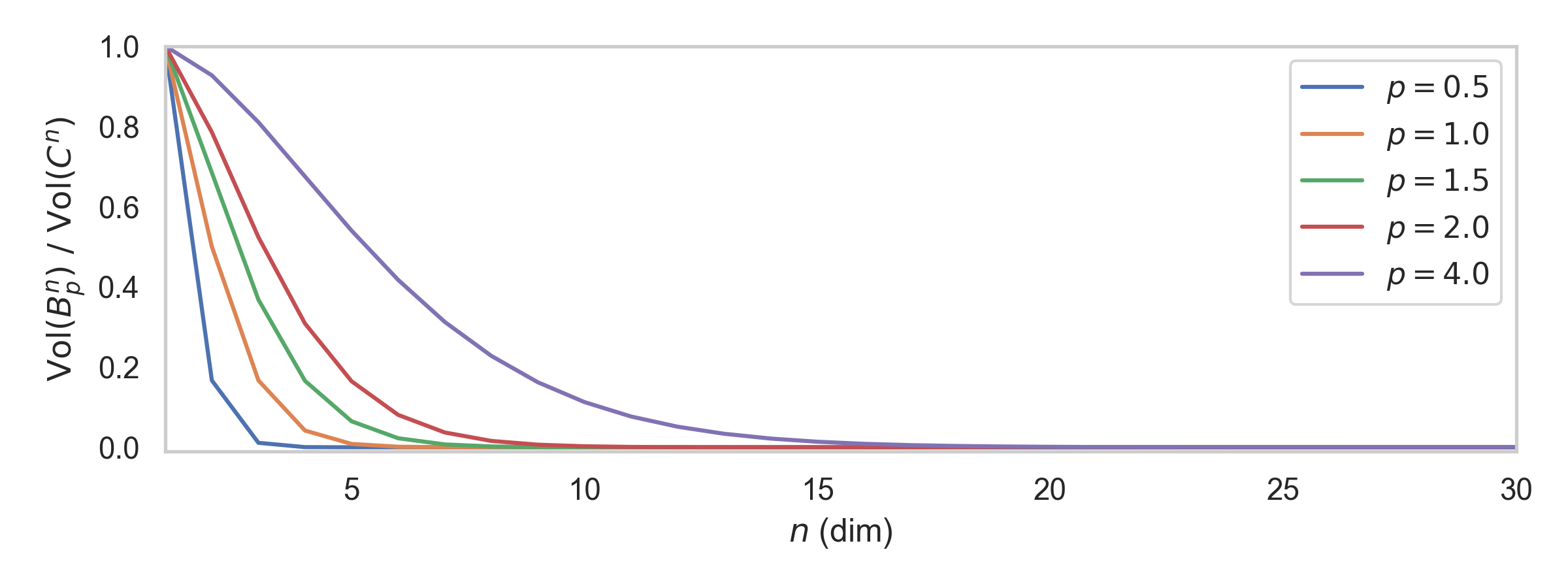
5. Second attempt

• \(n\) -dimensional Gaussian: \(X \sim \mathcal{N}(0, I)\)
• Observation: for \(O \in \mathrm{SO}(n)\): \[ X \sim OX \quad \Rightarrow \frac{X}{\lVert X \rVert_2} \sim \frac{OX}{\lVert X \rVert_2} = \frac{OX}{\lVert OX \rVert_2} \]
• Hence: \(X \, / \, \lVert X \rVert_2 \sim \mathcal{S}^{n-1}_2\)

6. Why did this trick work?

Spherical symmetry \(\Leftrightarrow\) " \(L_2\) -symmetry "

\[\mathcal{N}(x \mid 0, I) \propto e^{-\frac{\lVert x \rVert_2^2}{2}}\]

\(p\) - generalized Gaussian:

\[\mathcal{N}_p(x \mid 0, I) \propto e^{-\frac{\lVert x \rVert_p^p}{2}}\]

7. Recipe for L_p spheres

• Draw \(X \sim \mathcal{N}_p(x \mid 0, I)\).
• Then \[ X \, / \, \lVert X \rVert_p \sim \mathcal{S}^{n - 1}_p \]
• Drawing \(X\) can be done dimensionwise!

8. L_p spherical distributions

• \(L_p\) spherical RV: \[Z = R \times U, \quad U \sim \mathcal{S}_p^n, R > 0\]
• \(Z \sim \mathcal{S}_p^n\): \(\quad R = 1\).
• \(Z \sim \mathcal{N}_p\): \(\quad R^p \sim \chi^2(2n \, /\, p)\).
• \(Z \sim \mathcal{B}_p^n\): \(\quad \mathbb{P}[R < r] = \min\{r, 1\}^n\).

9. How special is our trick?

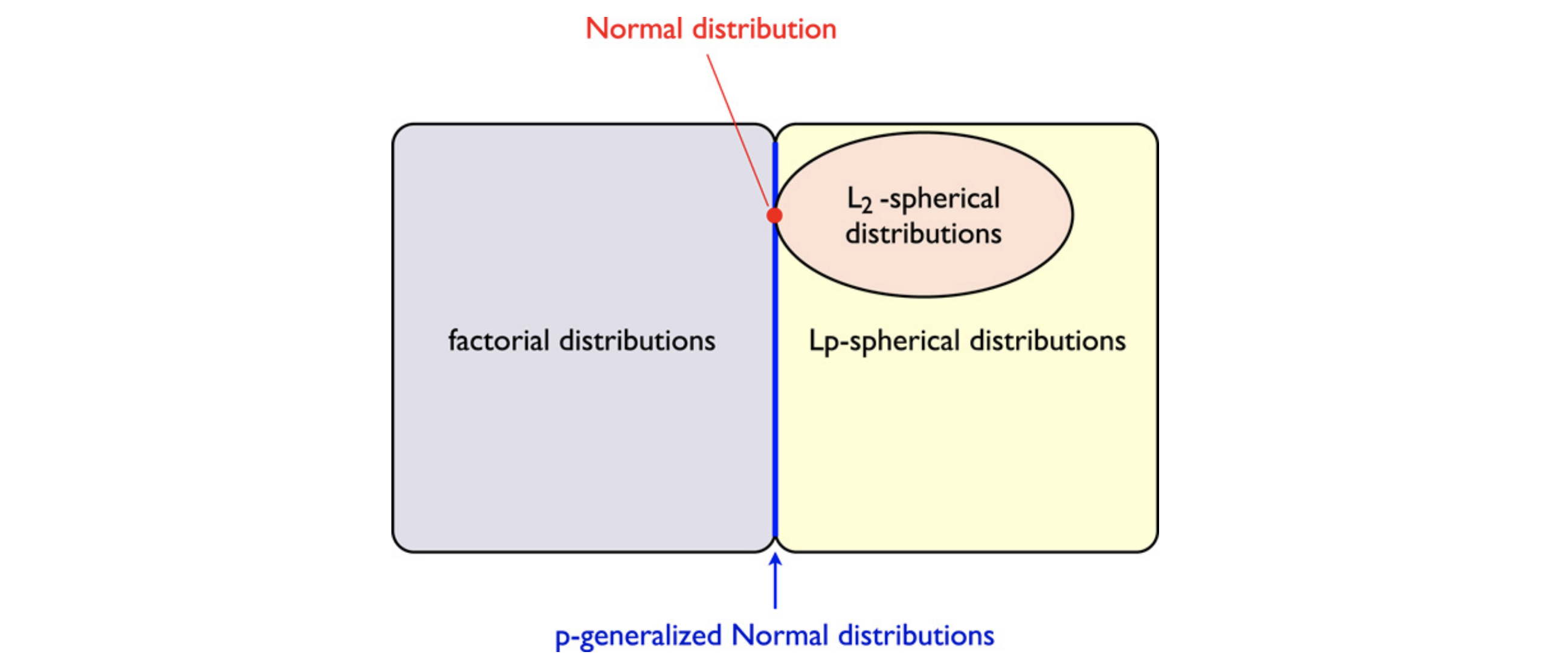
10. A third way for L_p balls

• Let \(U \sim \mathcal{S}^{n - 1}_p\)
• Then \(U = U_{1:n} = (U_1, \dots, U_{n})\)
• \(U_{1:k} \sim ?\)

Theorem: \(U_{1:n - p} \sim \mathcal{B}^{n - p}_p\)

11. References

• Wang, X. (2005). Volumes of generalized unit balls. Mathematics Magazine, 78(5), 390-395.
• Sinz, F., Gerwinn, S., & Bethge, M. (2009). Characterization of the p-generalized normal distribution. Journal of Multivariate Analysis, 100(5), 817-820.
• Barthe, F., Guédon, O., Mendelson, S., & Naor, A. (2005). A probabilistic approach to the geometry of the ℓpn-ball. The Annals of Probability, 33(2), 480-513.